支持向量机——Large Margin Classifier

支持向量机的目标是

[underbrace {min }_ heta left{ {Cleft[ {sumlimits_{i = 1}^m {{y^{left( i ight)}}{mathop{ m Cos} olimits} {t_1}left( {{ heta ^T}{x^{left( i ight)}}} ight) + left( {1 - {y^{left( i ight)}}} ight){mathop{ m Cos} olimits} {t_0}left( {{ heta ^T}{x^{left( i ight)}}} ight)} } ight] + frac{1}{2}sumlimits_{j = 1}^n { heta _j^2} } ight}]

下图分别是Cost₁(z)和Cost₀(z)的示意图

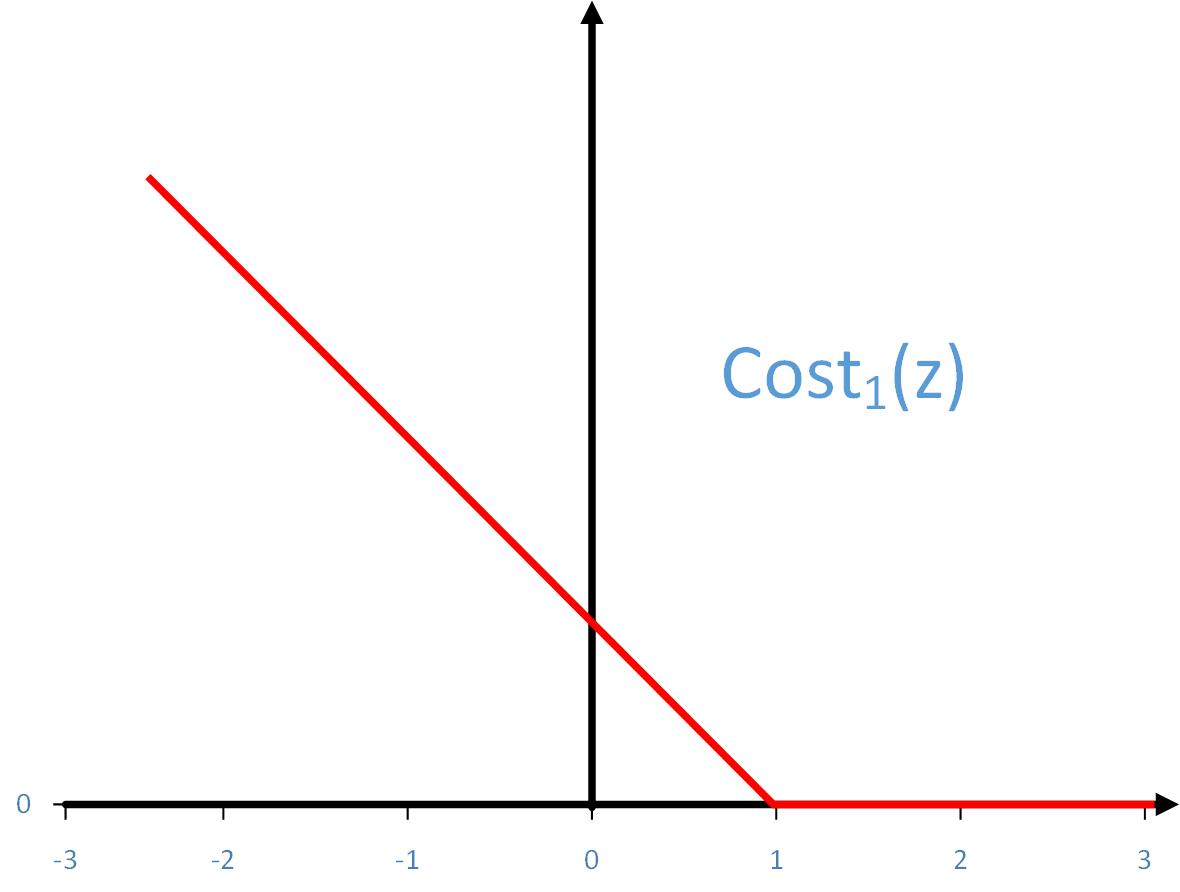
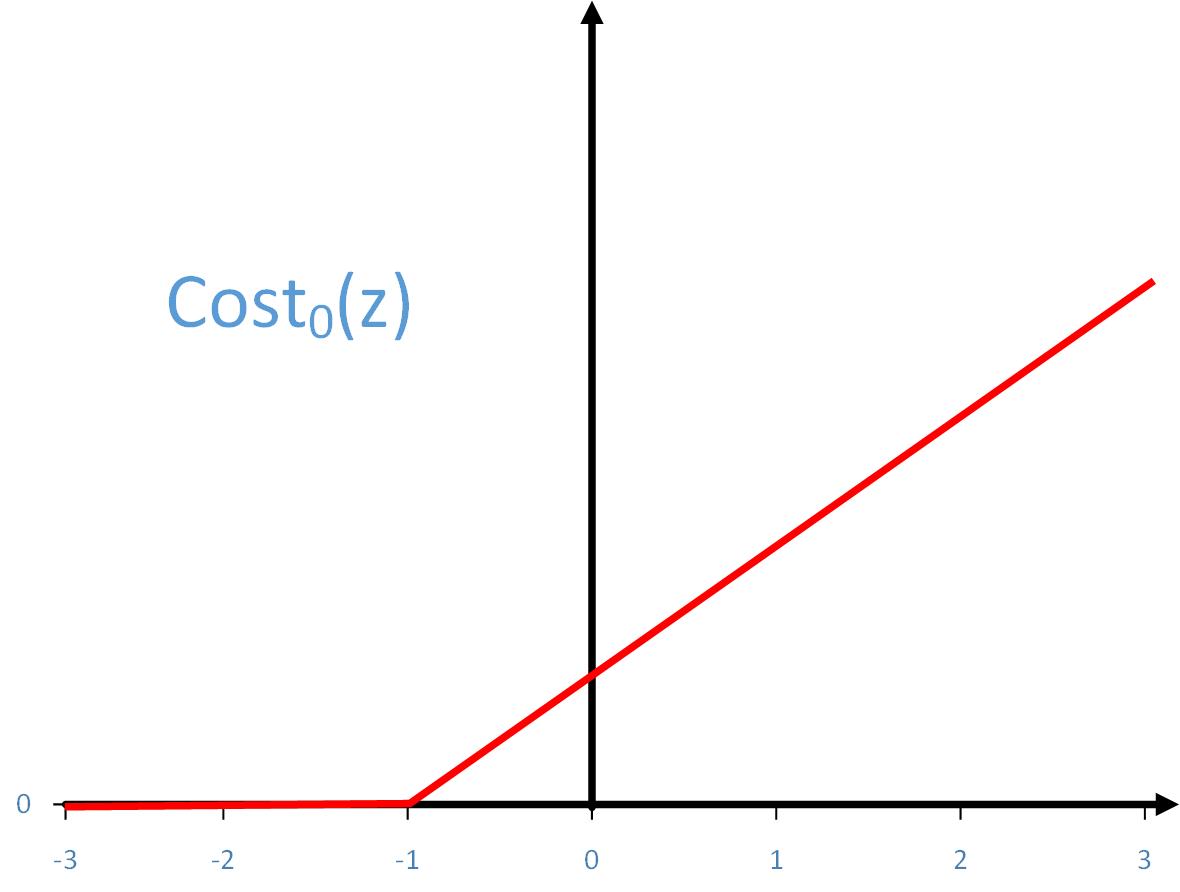
如果y=1，我们想要θ^Tx≥1（而不仅仅是θ^Tx≥0）

如果y=0，我们想要θ^Tx≤-1（而不仅仅是θ^Tx<0）

---

接下来考虑一种情况，当把式子中的C设置的非常大时

[underbrace {min }_ heta left{ {Cleft[ {sumlimits_{i = 1}^m {{y^{left( i ight)}}{mathop{ m Cos} olimits} {t_1}left( {{ heta ^T}{x^{left( i ight)}}} ight) + left( {1 - {y^{left( i ight)}}} ight){mathop{ m Cos} olimits} {t_0}left( {{ heta ^T}{x^{left( i ight)}}} ight)} } ight] + frac{1}{2}sumlimits_{j = 1}^n { heta _j^2} } ight}]

支持向量机为达到最小化的目的会试图将式子的第一部分（除了C）变得很小。

当y⁽ⁱ⁾=1时，得到的θ会使得θ^Tx≥1

当y⁽ⁱ⁾=0时，得到的θ会使得θ^Tx<-1

这样就会得到一个“比较有意思”的“decision boundary”。对于如下分类问题

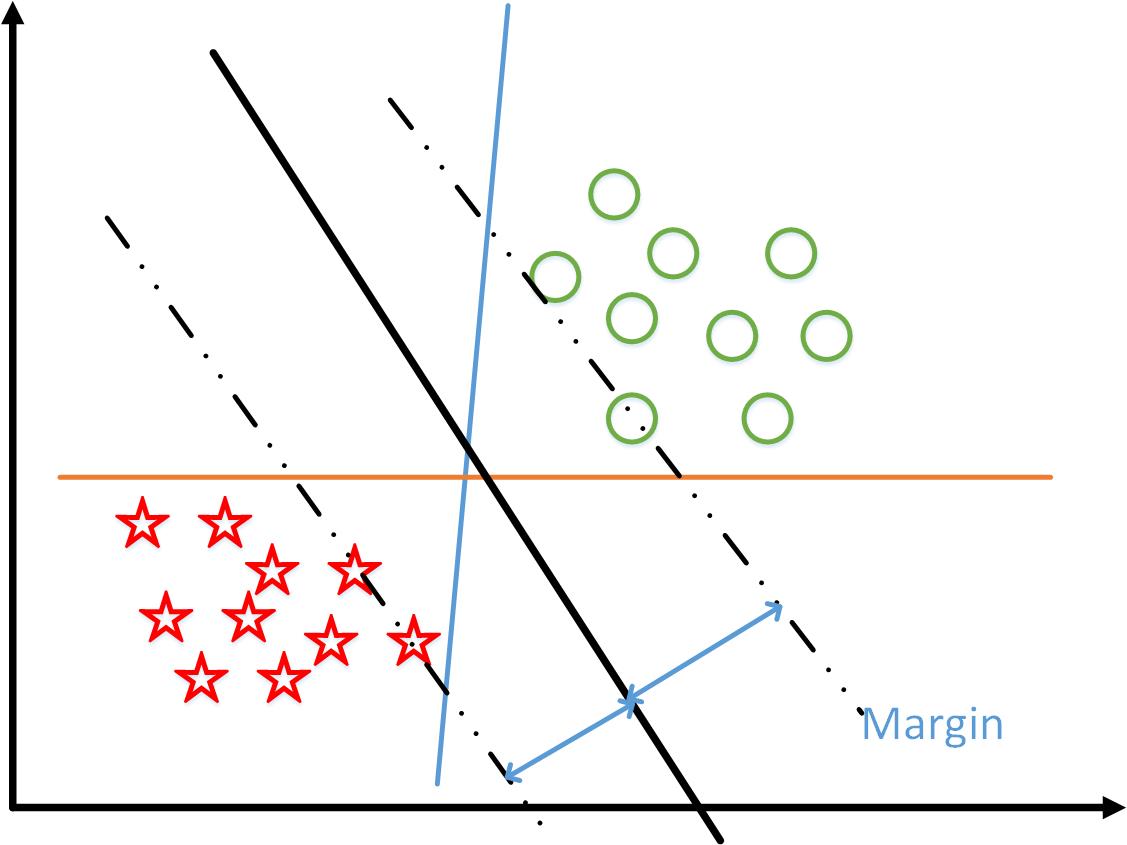
算法可以得到“蓝线”和“橙线”的分界线，也可以得到“黑色”分界线，支持向量机会得到黑色的线。

如果两条黑色虚线代表不同类的边界的话，支持向量机会得到距离两条虚线尽量远的一条直线。

---

需要注意的点

对于下面的分类问题，正常情况下应该得到蓝色的直线。

但是，当C非常大时，支持向量机会得到黄色的直线，因为它会得到距离两个类尽量远的直线。

如果取得C适当，支持向量机仍然会得到蓝色的先，即使出现非线性可分的情况（右侧红五角星）。