46.全排列
给定一个没有重复数字的序列，返回其所有可能的全排列。
示例:输入: [1,2,3]输出:[ [1,2,3], [1,3,2] [2,1,3], [2,3,1], [3,1,2], [3,2,1]]
1 class Solution {
2
3 List<List<Integer>> res = new ArrayList();
4
5 public List<List<Integer>> permute(int[] nums) {
6 if(nums == null || nums.length == 0) return res;
7 permutation(nums, 0);
8 return res;
9 }
10 public void permutation(int[] nums, int i){
11 if(i == nums.length-1){
12 ArrayList<Integer> list = new ArrayList();
13 for(int num : nums){
14 list.add(num);
15 }
16 res.add(list);
17 }else{
18 for(int j = i; j < nums.length; j++){
19 swap(nums, i, j);
20 permutation(nums, i+1);
21 swap(nums, i, j);
22 }
23 }
24 }
25 public void swap(int[] nums, int i, int j){
26 int temp = nums[i];
27 nums[i] = nums[j];
28 nums[j] = temp;
29 }
30 }
48.旋转图像
给定一个 n × n 的二维矩阵表示一个图像。将图像顺时针旋转 90 度。说明：你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
分析：转置+翻转
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
//转置
for(int i=0; i < n; i++){
for(int j=i; j < n; j++){
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
//翻转
for(int i=0; i<n; i++){
for(int j=0; j < n/2; j++){
int temp = matrix[i][j];
matrix[i][j] = matrix[i][n-1-j];
matrix[i][n-1-j] = temp;
}
}
}
}
49.字母异位词分组
给定一个字符串数组，将字母异位词组合在一起。字母异位词指字母相同，但排列不同的字符串。
示例:输入: ["eat", "tea", "ate", "nat", "bat"],输出:[ ["ate","eat","tea"], ["nat","tan"], ["bat"]]
说明：所有输入均为小写字母。 不考虑答案输出的顺序。
分析：字母异位词字母相同，若将字符转换成数组进行排序，则他们的排序结果相同。使用一个HashMap保存数据，key是排序字符串，value是一个列表，存储字母异位词。
1 class Solution {
2 public List<List<String>> groupAnagrams(String[] strs) {
3 if(strs == null || strs.length == 0) return new ArrayList();
4 Map<String,List> map = new HashMap();
5 for(String str : strs){
6 char[] ch = str.toCharArray();
7 Arrays.sort(ch);
8 String key = String.valueOf(ch);//排序后的字符串
9 if(!map.containsKey(key)){
10 map.put(key,new ArrayList());
11 }
12 map.get(key).add(str);
13 }
14 return new ArrayList(map.values());
15 }
16 }
53.最大子序和
给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和
示例:输入: [-2,1,-3,4,-1,2,1,-5,4],输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
分析：贪心：每一步做到最好，然后找出整个数组中最优值。先维护一个当前位置和最大值curMax，和一个当前位置和当前位置之前的和最大值allMax。curMax的取值通过当前位置加上或者不加上前面取值（取较大值，且当前位置的值必包含在和内）来得到。时间复杂度O(N) 空间复杂度 O(1)
1 class Solution {
2 public int maxSubArray(int[] nums) {
3 int curMax = nums[0], allMax = nums[0];
4 for(int i=1; i < nums.length; i++){
5 curMax = Math.max(nums[i], curMax + nums[i]);
6 allMax = Math.max(curMax, allMax);
7 }
8 return allMax;
9 }
10 }
55.跳跃游戏
给定一个非负整数数组，你最初位于数组的第一个位置。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个位置。
示例 1:输入: [2,3,1,1,4]输出: true
解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
示例 2:输入: [3,2,1,0,4]输出: false
解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。
方法一：递归——所有可能 （超时了……），一个位置判断为不行之后，之前的位置在遍历时还会到这个位置，重复判断。时间复杂度O(2^n)
1 class Solution {
2 public boolean canJump(int[] nums) {
3 return testJump(nums, 0);
4 }
5
6 public boolean testJump(int[] nums, int index){
7 if(index > nums.length) return false;
8 if(index == nums.length-1) return true;
9 for(int i = 1; i <= nums[index]; i++){//可能的跳数
10 if(testJump(nums, index + i)){
11 return true;
12 }
13 }
14 return false;
15 }
16 }
方法二：设置一个数组，有三个值-1，0，1。‘-1’表示该位置不能到达终点，‘0’表示初始未知，‘1’表示从该位置出发可以到达终点。为了重复判断，采取从右到左遍历方式。时间复杂度O(N^2) 空间复杂度 O(N)
1 class Solution {
2 public boolean canJump(int[] nums) {
3 int len = nums.length;
4 int[] standard = new int[len];//默认是0
5 //最后一个位置肯定是1
6 standard[len-1] = 1;
7 //从右往左遍历
8 for(int i = len-2; i>=0; i--){
9 //当前位置有nums[i]种跳法
10 for(int jump = 1; jump <= nums[i] && i + jump < len; jump++){
11 if(standard[i+jump] == 1){
12 standard[i] = 1;
13 break;
14 }
15 }
16 }
17 return standard[0] == 1;
18 }
19 }
方法三：贪心，位置 i 能够跳到另一个位置 j 则需要条件：i + nums[i] >= j。根据这一条件我们可以从右往左不断寻找满足这样条件的位置，例如
[9,4,2,1,0,2,0]，最后一个位置nums[6]=0，目的索引为i=6，从右往左寻找，发现 5 + nums[5] = 7 > 6，所以能够从i=5位置跳到i=6，此时将目的位置设置为i=5。再次寻找，发现 0 + nums[0] = 9 > 7，即能够从i=0位置跳到i=5，此时将目的位置设置为i=0，结束！虽然从i=0也能直接跳到i=6，但是只要有一种跳法就可以，如果一个点能够忽略中间“跳板”跳到终点，那么这个点肯定也能够通过“跳板”跳到终点，本方法采用的是贪心算法，尽可能多的跳。时间复杂度O(N) 空间复杂度 O(1)
1 class Solution {
2 public boolean canJump(int[] nums) {
3 int len = nums.length;
4 int destination = len - 1;
5 for(int i = len - 2; i >= 0; i--){
6 destination = (i + nums[i]) >= destination ? i : destination;
7 }
8 return destination == 0;
9 }
10 }
56.合并区间
给出一个区间的集合，请合并所有重叠的区间。(二维数组是n行2列)
示例 1:输入: [[1,3],[2,6],[8,10],[15,18]]，输出: [[1,6],[8,10],[15,18]]，解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:输入: [[1,4],[4,5]]，输出: [[1,5]]，解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
分析：什么样的区间需要合并？例如[a,b]、[c,d]，如果 c<=b<=d则两个区间有重合部分，需要合并。那合并后的区间应该是什么样的呢？ 合并后的区间应该是 [ min(a,c) , max(b,d) ]。此题应该先将二维数组进行排序，避免合并区间进行多次循环，那么此时合并的条件就变成 !(c>b)。合并后的区间为[a , max(b,d)]。因为合并区间需要存入存出并且不知道合并后的区间个数，因此采用一个LinkedList临时存储合并后的区间，最后使用toArray返回结果。
1 class Solution {
2 public int[][] merge(int[][] intervals) {
3 LinkedList<int[]> list = new LinkedList();
4 if(intervals == null || intervals.length == 0) return list.toArray(new int[0][]);
5 //根据数组首位元素进行排序
6 Arrays.sort(intervals, new Comparator<int[]>(){
7 public int compare(int[] o1, int[] o2){
8 return o1[0] - o2[0];//根据数组区间左位置排序
9 }
10 });
11 list.add(intervals[0]);
12 for(int i = 1; i < intervals.length; i++){
13 if(intervals[i][0] > list.getLast()[1]){//c>b 直接在list填入
14 list.add(intervals[i]);
15 }else{//需要合并区间，只要将list最后一个元素的右位置取两个中的最大值
16 list.getLast()[1] = Math.max(intervals[i][1], list.getLast()[1]);
17 }
18 }
19 return list.toArray(new int[0][0]);
20
21 }
22 }
62. 不同路径
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。问总共有多少条不同的路径？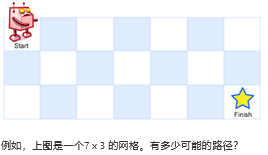
说明：m 和 n 的值均不超过 100。
示例 1:输入: m = 3, n = 2，输出: 3
解释:从左上角开始，总共有 3 条路径可以到达右下角。1. 向右 -> 向右 -> 向下2. 向右 -> 向下 -> 向右3. 向下 -> 向右 -> 向右
示例 2:输入: m = 7, n = 3，输出: 28
分析：如果机器人位于（i，j）位置，则下一步可能要走的位置( i+1 , j ) , ( i , j+1 )。感觉和全排列相似，使用递归回溯方法
法一：递归 超时
1 class Solution {
2 int res = 0;
3 public int uniquePaths(int m, int n) {
4 path(0,0,m,n);
5 return res;
6 }
7 public void path(int i, int j, int m, int n){
8 if(i == m-1 && j == n-1){
9 res++;
10 }
11 if(i>=m||j>=n){
12 return;
13 }
14 path(i+1,j,m,n);
15 path(i,j+1,m,n);
16 return;
17 }
18 }
法二：动态规划
定义一个二维数组dp[][]，表示到从出发点到当前位置有多少种走法，因为机器人只能向右或者向下移动，所以d[0][]，d[][0]都为1（一直向下，或者一直向右）。当i!=0,j!=0时，到达（i，j）位置只能通过（i-1,j）和（i,j-1）两个位置到达，所以dp[i][j] = dp[i-1][j] + dp[i][j-1].
1 class Solution {
2 public int uniquePaths(int m, int n) {
3 int[][] dp = new int[m][n];
4 for(int i=0;i<m;i++) dp[i][0] = 1;
5 for(int i=0;i<n;i++) dp[0][i] = 1;
6 for(int i=1;i<m;i++){
7 for(int j=1;j<n;j++){
8 dp[i][j] = dp[i-1][j]+dp[i][j-1];
9 }
10 }
11 return dp[m-1][n-1];
12 }
13 }
64.最小路径和
给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。
说明：每次只能向下或者向右移动一步。
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
] 输出: 7解释: 因为路径 1→3→1→1→1 的总和最小。
分析：根据上题可以轻松想到动态规划(可以新建一个dp二维数组，也可以直接在原来数组上修改，看实际应用是是否允许修改原数组)
1 class Solution {
2 public int minPathSum(int[][] grid) {
3 int m = grid.length;
4 int n = grid[0].length;
5 int[][] dp = new int[m][n];
6 dp[0][0] = grid[0][0];
7 for(int i=1;i<m;i++) dp[i][0] = dp[i-1][0] + grid[i][0];
8 for(int j=1;j<n;j++) dp[0][j] = dp[0][j-1] + grid[0][j];
9 for(int i=1;i<m;i++){
10 for(int j=1;j<n;j++){
11 dp[i][j] = grid[i][j] + Math.min(dp[i-1][j], dp[i][j-1]);
12 }
13 }
14 return dp[m-1][n-1];
15 }
16 }
70.爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？注意：给定 n 是一个正整数。法一：递归 超时（这玩意能少就少用）
1 class Solution {
2 public int climbStairs(int n) {
3 if(n<=3){
4 return n;
5 }else{
6 return climbStairs(n-1) + climbStairs(n-2);
7 }
8 }
9 }
法二：动态规划，使用数组
1 class Solution {
2 public int climbStairs(int n) {
3 if(n<=3){
4 return n;
5 }
6 int[] dp = new int[n];
7 dp[0] = 1;
8 dp[1] = 2;
9 for(int i=2;i<n;i++){
10 dp[i] = dp[i-1] + dp [i-2];
11 }
12 return dp[n-1];
13 }
14 }
法三：斐波那契数列，不需要数组
1 class Solution {
2 public int climbStairs(int n) {
3 if(n<=3){
4 return n;
5 }
6 int first = 1;
7 int second = 2;
8 for(int i=3;i<=n;i++){
9 int third = first + second;
10 first = second;
11 second = third;
12 }
13 return second;
14 }
15 }
72.编辑距离
给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作： 插入一个字符、删除一个字符、替换一个字符
示例 1:输入: word1 = "horse", word2 = "ros"，输出: 3
解释: horse -> rorse (将 'h' 替换为 'r'，rorse -> rose (删除 'r')，rose -> ros (删除 'e')
示例 2:输入: word1 = "intention", word2 = "execution"，输出: 5
解释: intention -> inention (删除 't')，inention -> enention (将 'i' 替换为 'e')，enention -> exention (将 'n' 替换为 'x')，exention -> exection (将 'n' 替换为 'c')，exection -> execution (插入 'u')
分析：？这题不会分析，直接题解了。。。官方使用动态规划算法，递归也能解决，不过重复率过高。
首先建立一个二维数组dp[i][j]表示word1的前i个字母和word2的前j个字母之间的最短编辑距离。按照以往经验，从前往后推dp数组元素，根据前面的数组元素确定当前最短编辑距离。那么怎么确定当前元素呢？已知对一个单词可以有三种操作：删除、插入、替换。
如果当前i位置和j位置的字符相同，即word1[i] = word2[j]，那么这两个字符不需要任何操作，dp[i][j] = dp[i-1][j-1]。
如果当前i位置和j位置的字符相同，即word1[i] != word2[j]，那么当前字符应该如何操作呢？我们来看dp[i][j]之前的操作。
① dp[i-1][j-1]：如果使得dp[i][j] = dp[i-1][j-1]+1，那么就是当前字符进行替换。
② dp[i][j-1]：如果使得dp[i][j] = dp[i][j-1]+1，那么就是在word1[i]字符进行插入操作，这样word1[i]就和word2[j]匹配了，前移j一个，继续和i比较。
===》》》》》
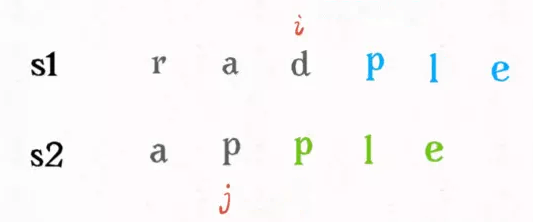③ dp[i-1][j-1]：如果使得dp[i][j] = dp[i-1][j]+1，那么就是在word1[i]字符进行删除操作，保持j位置不动，i往前移动一个。
已经确定了之前的三个操作，那么如何选择呢，当然是选择最小的了！
1 class Solution {
2 public int minDistance(String word1, String word2) {
3 int len1 = word1.length();
4 int len2 = word2.length();
5 int[][] dp = new int[len1+1][len2+1];
6 //开始填入0行0列初始数据
7 for(int i=0;i<=len1;i++) dp[i][0] = i;//只进行删除操作
8 for(int i=0;i<=len2;i++) dp[0][i] = i;
9 //计算dp[][]
10 for(int i=1;i<=len1;i++){
11 for(int j=1;j<=len2;j++){
12 if(word1.charAt(i-1)==word2.charAt(j-1)){
13 dp[i][j] = dp[i-1][j-1];//当前相等，就直接往前移动一个
14 }else{
15 dp[i][j] = Math.min(dp[i-1][j-1],Math.min(dp[i][j-1],dp[i-1][j]))+1;//替换、插入、删除
16 }
17 }
18 }
19 return dp[len1][len2];
20
21 }
22 }