刷题篇--热题HOT 31-40

75.颜色分类

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
注意:不能使用代码库中的排序函数来解决这道题。
示例:输入: [2,0,2,1,1,0]输出: [0,0,1,1,2,2]
分析：数组只有三个（常数个）元素，那么只要计算012的个数然后填入原数组。

class Solution {
    public void sortColors(int[] nums) {
        int numOfZero = 0, numOfOne = 0, numOfTwo = 0;
        for(int i=0;i<nums.length;i++){
            if(nums[i]==0){
                numOfZero++;
            }else if(nums[i]==1){
                numOfOne++;
            }else{
                numOfTwo++;
            }
        }
        int index = 0;
        while(index < numOfZero){
            nums[index] = 0;
            index++;
        }
        while(index < numOfOne+numOfZero){
            nums[index] = 1;
            index++;
        }
        while(index < numOfTwo+numOfOne+numOfZero){
            nums[index] = 2;
            index++;
        }
    }
}

 法二：定义三个指针p0，p1，cur分别代表着p0索引左边全是0，p2索引右边全是2，p0~p2索引和之间全是1.所以要确定p0和p2的位置就可以了。

cur初始定义为0，当nums[cur]=2时，就交换cur和p2的元素，p2-1。当nums[cur] = 0时，交换cur和p0的元素，cur+1，p0+1。如果nums[cur]=1，则将cur右移。直到cur>p2.

class Solution {
    public void sortColors(int[] nums) {
        int p0 = 0, p2 = nums.length-1, cur = 0;
        while(cur <= p2){
            if(nums[cur]==0){
                swap(nums, cur, p0);
                cur++;
                p0++;
            }else if(nums[cur]==1){
                cur++;
            }else{
                swap(nums, cur, p2);
                p2--;
            }
        }
    }
    public void swap(int[] nums, int i, int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    } 
}

 

 76.最小覆盖字串

给你一个字符串 S、一个字符串 T，请在字符串 S 里面找出：包含 T 所有字母的最小子串。

示例：输入: S = "ADOBECODEBANC", T = "ABC",输出: "BANC"
说明：如果 S 中不存这样的子串，则返回空字符串 ""。如果 S 中存在这样的子串，我们保证它是唯一的答案。
分析：此问题有俩个点：

　　1.如何确定包含字符串T：使用HashMap，key为字符串T的字符，value是字符出现次数。滑动窗口right++时，如果S[right]是T的字符，则将value-1，滑动窗口left++时，如果如果S[left]是T的字符，则将value+1。如果HashMap所有的value都是0，则说明left~right的字串包含T。

　　2.如何保证最小字串：使用滑动窗口（一般用于最多、最少连续等关键词），定义left、right指针，right用于扩展，left用于收缩。确定最小窗口，则为结果。

class Solution {
    public String minWindow(String s, String t) {
        int left = 0, right = 0;//滑动窗口左右两索引
        int minLeft = 0, minRight = -1;//保存最小子串的左右两边索引
        int minLen = s.length();//默认最小字串长度
        Map<Character, Integer> map = new HashMap();
        //初始map
        for(int i=0;i<t.length();i++){
            char ch = t.charAt(i);
            map.put(ch, map.getOrDefault(ch,0)+1);
        }
        //滑动窗口
        while(right < s.length()){
            char chOfRight = s.charAt(right);
            //移动右指针，并判断是否已经包含T
            if(map.containsKey(chOfRight)){
                //当前相同字符次数减一
                map.put(chOfRight,map.get(chOfRight)-1);
                //判断是否全包含T
                while(match(map)){
                    //移动左指针
                    char chOfLeft = s.charAt(left);
                    //当前相同字符次数加一
                    if(map.containsKey(chOfLeft)){
                        map.put(chOfLeft,map.get(chOfLeft)+1);
                    }
                    //修改最小字串索引、长度
                    if((right-left+1) <= minLen){
                        minLen = right-left+1;
                        minLeft = left;
                        minRight = right;
                    }
                    left++;
                }
            }
            right++;
        }
        return s.substring(minLeft, minRight+1);
    }
    //判断map的value是否为空
    public boolean match(Map<Character, Integer> map){
        for(Integer value : map.values()){
            if(value > 0){
                return false;
            }
        }
        return true;
    }
}

【优化】实践复杂度为O(mn)，空间复杂度为O(m)。上面解法使用的是map存储T的字符次数。实际上可以使用一个int数组，索引是字符减去字符0之后的ascii值，数组值是出现的字符出现次数。那么如何判断T已经包含在left~right内呢？可以设置一个整数count = T.length()，每当right遍历到T中的字符，就减一，每当left遍历到就加一。代码此处省略

78.子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。说明：解集不能包含重复的子集。
示例:输入: nums = [1,2,3]；输出:[ [3],[1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]
分析：类似全排列，只不过将全排列最后存储结果变为每小一步都存储结果。

结果输出为 [ [], [1], [1,2], [1,2,3], [1,3], [2], [2,3], [3] ]

class Solution {
    List<List<Integer>> res = new ArrayList();
    public List<List<Integer>> subsets(int[] nums) {
        if(nums == null || nums.length == 0) return res;
        List<Integer> list = new ArrayList();
        helper(nums, 0, list);
        return res;
    }
    public void helper(int[] nums, int start, List<Integer> list){
        res.add(new ArrayList(list));
        for(int i = start ; i < nums.length ; i++){
            list.add(nums[i]);
            helper(nums, i+1, list);
            list.remove(list.size()-1);
        }
    }
}

 

 79.单词搜索

给定一个二维网格和一个单词，找出该单词是否存在于网格中。单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]
给定 word = "ABCCED", 返回 true.
给定 word = "SEE", 返回 true.
给定 word = "ABCB", 返回 false.
分析：回溯+递归

class Solution {
    public boolean exist(char[][] board, String word) {
        int index = 0;
        int m = board.length;
        int n = board[0].length;
        boolean[][] visited = new boolean[m][n];
        for(int i=0;i<m;i++){
            for( int j=0;j<n;j++){
                if(board[i][j] == word.charAt(index)){
                    boolean res = isExist(board, index, word, i, j, visited);
                    if(res) return true;
                }
            }
        }
        return false;
    }
    public boolean isExist(char[][] board, int index, String word, int i, int j, boolean[][] visited){
        if(index == word.length()) return true;
        if(i<0 || i >= board.length || j<0 || j>=board[0].length || visited[i][j] || board[i][j] != word.charAt(index)){
            return false;
        } 
        visited[i][j] = true;
        if(isExist(board, index+1, word, i-1, j, visited)||
           isExist(board, index+1, word, i+1, j, visited)||
           isExist(board, index+1, word, i, j-1, visited)||
           isExist(board, index+1, word, i, j+1, visited))
        {
            return true;        
        }
        visited[i][j] = false;//回溯
        return false;
    }
}

 

 84.柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

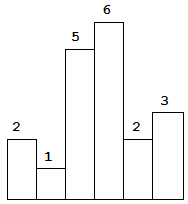
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。 

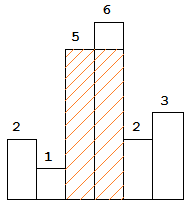
 图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

 法一：分治，最大矩形面积取决于最低的柱子高度和两边之间的距离。先寻找出最低的柱子，以此柱子为界，再计算左右两边，取出最低柱子和左右边面积最大值。递归。

class Solution {
    public int largestRectangleArea(int[] heights) {
        return calculateArea(heights, 0, heights.length-1);
    }
    public int calculateArea(int[] heights, int start, int end){
        if(start > end) return 0;
        //计算最小值
        int minHeightsIndex = start;
        for(int i = start; i <= end; i++){
            if(heights[i] < heights[minHeightsIndex]){
                minHeightsIndex = i;
            }
        }
        //返回计算三个面积的最大值
        return Math.max(heights[minHeightsIndex]*(end-start+1),
               Math.max(calculateArea(heights,start,minHeightsIndex-1),calculateArea(heights,minHeightsIndex+1,end)));
    }
}

 法二：包含当前柱子的最大矩形示意图如下：

 

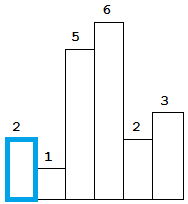
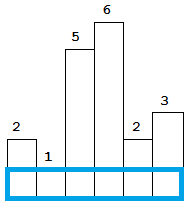
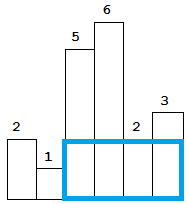
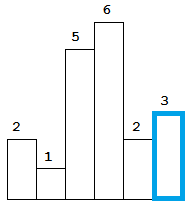
 图解：

①先将2存入栈内，左边沿的左边是-1；

② 1小于2，那么2的左边沿和右边沿都能确定了，计算2的最大矩形面积，压入1；

③ 5大于1，则5的左边沿能够确定，右边沿未知，则压入5；

④ 6和5同样操作；

⑤ 2小于6，那么6的左边沿和右边沿能够确定，则计算面积并弹出，继续比较，2小于5，则5的左右边沿也能够确定，同6操作，继续比较，2大于1，压入2；

⑥ 3大于 2，直接压入；

⑦处理栈内剩下元素，这些元素当初是因为右边沿无法确定而一直存在栈内的，但是数组遍历完之后，这些栈内元素的右边沿都是数组的长度，左边沿是左边相邻的元素。【这里的压入弹出的数据时数组索引，而不是值】

　　只需要计算上图中的六个面积的最大值即为答案。那面积如何求得呢？通过观察发现，矩形的左边沿是左边第一个小于本柱子的右边，右边沿是右边第一个小于本柱子的左边。

　　那么如何寻找呢？使用单调栈，栈内元素从小到大排列，这也就保证可以存储到左边沿。

　　那么右边沿如何判断呢？如果遍历到的柱子高度低于栈顶元素，也就是说明以栈顶元素为核心的矩形找到了，遍历到的柱子就是右边沿右边一个位置。当然，这个遍历到的柱子可能是很多柱子的右边沿的右边，需要while循环。这样就可以得知左边沿（）和右边沿了，只要在弹出过程中保存最大面积即可。

　　遍历结束时如果最后栈内剩下元素，那么一定是递增的，右边沿是数组长度，例如上例就会剩下 1  4 5分别代表高度1 2 3，此时再使用一个while循环，不断计算面积保存最大值。

class Solution {
    public int largestRectangleArea(int[] heights) {
        Stack<Integer> stack = new Stack();
        stack.push(-1);
        int maxArea = 0;

        //遍历
        for(int i=0; i < heights.length; i++){
            //左边沿位置 stack.pop().peek(),右边沿位置i-1
            while(stack.peek() != -1 && heights[i] <= heights[stack.peek()]){
                maxArea = Math.max(maxArea, heights[stack.pop()]*(i-1-stack.peek()));
            }
            //不管有没有上述操作都要压入
            stack.push(i);
        }

        //处理剩下的数据，右边沿是heights.length-1，即最后一个元素
        while(stack.peek() != -1){
            maxArea = Math.max(maxArea, heights[stack.pop()]*(heights.length-stack.peek()-1));
        }

        return maxArea;
    }
}

 85.最大矩形

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。
示例:输入:
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]       输出: 6

分析：面积如何计算？矩形左上角位置和右下角位置索引计算。

将本题转换为84题。

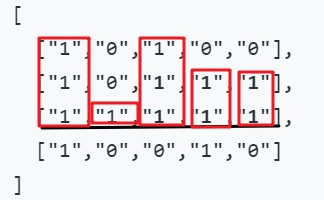
① 利用一维数组存储从上往下，以每行为底的每列高度；

②遍历matrix每一行，利用84题中栈方法更新最大面积；

class Solution {
    public int maximalRectangle(char[][] matrix) {
        if(matrix.length == 0) return 0;
        int maxArea = 0;
        int[] heights = new int[matrix[0].length];
        //利用matrix数组存储从上往下，以每行为底的每列高度；
        for(int i=0;i<matrix.length;i++){
            for(int j=0;j<matrix[0].length;j++){
                heights[j] = matrix[i][j] == '1' ? heights[j] + 1 : 0;
            }
            maxArea = Math.max(maxArea, largestRectangleArea84(heights));
        }
        return maxArea;
    }
    public int largestRectangleArea84(int[] heights) {
          Stack<Integer> stack = new Stack();
          stack.push(-1);
          int maxArea = 0;
          //遍历
          for(int i=0; i < heights.length; i++){
             //左边沿位置 stack.pop().peek(),右边沿位置i-1
            while(stack.peek() != -1 && heights[i] <= heights[stack.peek()]){
                 maxArea = Math.max(maxArea, heights[stack.pop()]*(i-1-stack.peek()));
             }
             //不管有没有上述操作都要压入
             stack.push(i);
         }
         //处理剩下的数据，右边沿是heights.length-1，即最后一个元素
         while(stack.peek() != -1){
             maxArea = Math.max(maxArea, heights[stack.pop()]*(heights.length-stack.peek()-1));
         }
         return maxArea;
     }
}

94. 二叉树的中序遍历

递归

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    
    public List<Integer> inorderTraversal(TreeNode root) {
        ArrayList<Integer> res = new ArrayList();
        helper(root,res);
        return res;
    }
    public void helper(TreeNode root, List<Integer> res){
        if(root == null) return;
        helper(root.left, res);
        res.add(root.val);
        helper(root.right, res);
    }
}

 非递归

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        ArrayList<Integer> res = new ArrayList();
        Stack<TreeNode> stack = new Stack();
        TreeNode cur = root;
        while(cur != null || !stack.empty()){
            while(cur!=null){
                stack.push(cur);
                cur = cur.left;
            }
            cur = stack.pop();
            res.add(cur.val);
            cur = cur.right;
        }
        return res;
    }
}

 97.不同的二叉搜索树

给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

 示例:输入: 3输出: 5
解释:给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

   1          3     3      2      1
             /       /      /        
     3     2     1      1    3      2
    /      /                             
   2     1          2                     3

分析：看了解析，发现数个数学归纳题。1…n数列，如果取中间i为根节点，则1…i-1，i+1…n分别为左子树和右子树。

 设置两个函数：

　　G(n)：长度为n的序列的不同二叉搜索树的个数。

 　   F(i,n)：以i为根的不同二叉搜索树的个数。

易知：G(n) = F(1,n)+F(2,n)+F(3,n)+…+F(n-1,n)+F(n,n)，G(0) = 1 , G(1) = 1;

 　　   F(i,n) = G(i-1)*G(n-i)

综上：G(n) = ΣG(i-1)*G(n-i)，i=1,2,...,n。例如G(4) = G(0)*G(4) + G(1)*G(3) + G(2)*G(2) + G(3)*G(1)

class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n+1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2 ; i <= n ; i++){
            for(int j=1;j<=i;j++){
                dp[i] += dp[j-1]*dp[i-j]; 
            } 
        }
        return dp[n];
    }
}

实际上，G(n)函数是卡塔兰数 G(n+1) = (2(2n+1)/(n+2))*G(n)

class Solution {
    public int numTrees(int n) {
        long res = 1;
        for(int i=0;i<n;i++){
            res = res*2*(2*i+1)/(i+2); 
        }
        return (int)res;
    }
}

98.验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征：节点的左子树只包含小于当前节点的数；节点的右子树只包含大于当前节点的数； 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:
    2
   /
  1   3
输出: true
示例 2:
输入:
    5
   /
  1   4
     /
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。根节点的值为 5 ，但是其右子节点值为 4 。

分析：一个合格的搜索二叉树的中序遍历一定是一个单调递增的数列，例如示例一：123√，示例二：15346×。

   5
   /
  1   6
       /
     4   7

再例如上例：15467×。因此在中序遍历的时候，存储最后一个遍历的节点值temp，判断下一个遍历的节点值是否大于temp，如果大于，则继续遍历，直至遍历完。如果小于则返回false。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {
        Stack<TreeNode> stack = new Stack();
        double temp = -Double.MAX_VALUE;
        TreeNode cur = root;
        while(cur != null || !stack.empty()){
            while(cur!=null){
                stack.push(cur);
                cur = cur.left;
            }
            cur = stack.pop();
            if(cur.val <= temp) return false;
            temp = cur.val;
            cur = cur.right;
        }
        return true;
    }
}

101.对称二叉树

给定一个二叉树，检查它是否是镜像对称的。例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

     1
   /   
  2     2
 /     /
3  4  4  3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
    1
   /
  2   2
      
   3    3
递归

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        return helper(root, root);
    }
    public boolean helper(TreeNode left, TreeNode right){
        if(left==null&&right==null){
            return true;
        }else if(left == null || right == null || left.val != right.val){
            return false;
        }else{
            return helper(left.left,right.right) && helper(left.right,right.left);
        }
    }
}

//迭代-类似于层序遍历，使用队列

class Solution {
    public boolean isSymmetric(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList();
        queue.add(root);
        queue.add(root);
        while(!queue.isEmpty()){
            TreeNode node1 = queue.poll();
            TreeNode node2 = queue.poll();
            if(node1 == null && node2 == null) continue;
            if(node1 == null || node2 == null || node1.val != node2.val) return false;
            queue.add(node1.left);
            queue.add(node2.right);
            queue.add(node1.right);
            queue.add(node2.left);
        }
        return true;
    }
}