并查集
一般的并查集,是只带一种属性的,即指向,pre[i]=i,代表父节点,添加一个扩展的属性,比如poj 1182 ,一个节点x会存在两个属性,一个pre,一个relation ,pre代表该节点的父节点指向,relation代表与父节点之间的关系,主要是在合并的时候维护了关系的传递性,通过扩展出来的属性来维护传递性。
而并查集的难点在于维护传递性的公式的推导,例题poj 1182
题目如下:
食物链
|
Time Limit: 1000MS |
Memory Limit: 10000K |
|
|
Total Submissions: 89688 |
Accepted: 26936 |
Description
动物王国中有三类动物A,B,C,这三类动物的食物链构成了有趣的环形。A吃B, B吃C,C吃A。
现有N个动物,以1-N编号。每个动物都是A,B,C中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述:
第一种说法是"1 X Y",表示X和Y是同类。
第二种说法是"2 X Y",表示X吃Y。
此人对N个动物,用上述两种说法,一句接一句地说出K句话,这K句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
1) 当前的话与前面的某些真的话冲突,就是假话;
2) 当前的话中X或Y比N大,就是假话;
3) 当前的话表示X吃X,就是假话。
你的任务是根据给定的N(1 <= N <= 50,000)和K句话(0 <= K <= 100,000),输出假话的总数。
Input
第一行是两个整数N和K,以一个空格分隔。
以下K行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中D表示说法的种类。
若D=1,则表示X和Y是同类。
若D=2,则表示X吃Y。
Output
只有一个整数,表示假话的数目。
Sample Input
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
Sample Output
3
【思路】:
读完这个题目,我们可以先给出一个结构体
typedef struct NODE
{
int parents;
int relation;
} node;
parents代表该节点的父节点,而relations这代表这个节点到其父节点的关系,通过题意我们容易得到存在被吃与同类的关系
X->Y
即0 同类, 1 x被y吃 , 2 y被x吃
题意要我们求的是假话有多少?
那我们要求的就是在合并的过程,有多少是矛盾的。
那么我们应该来研究下合并究竟是如何进行的,在第一个属性域,就是普通的并查集的连接,而在连接过程中,第二属性关系域该如何传递呢?
先来看第一种情况,即查找压缩路径的时候,如何压缩?
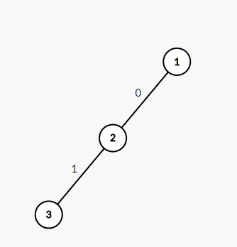
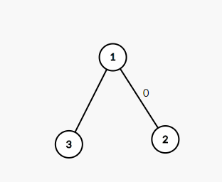
3这个节点与爷爷节点1的关系是什么呢?
权值(即relation)1 代表x被y吃 那么3 被 2 吃
权值(即relation)0 代表同类 那么 1 与 2同类
所以结果应该是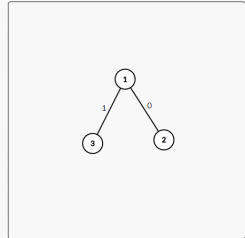
我们可以得到关系的函数为 假设数组为data
那么即 data[a].relation=(data[a].relation+data[b].relation)%3
你可能会对这个公式有所怀疑,那么我就来枚举下压缩路径的全部情况
那么我们假设
父亲节点与爷爷节点的关系数值为i
儿子节点与父亲节点的关系数值为j
父亲节点的relation 儿子节点的relation 爷爷节点与儿子节点的关系(即更新后的儿子节点的relation)
0 0 0
0 1 1
0 2 2
1 0 1
1 1 2
1 2 0
2 1 0
2 0 2
2 2 1
接下来,我们来看下合并操作
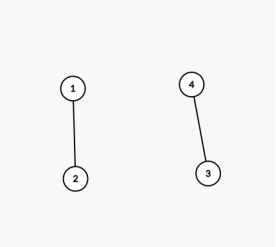
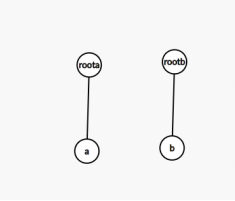
按照普通并查集的思路,假设我们要合并2 ,3这两个节点,那么我们应该先对2 ,3查询,查询这两个节点是不是位于一个集合中。(即查询这两个节点的祖先节点,看祖先节点是否相同)。
这时候就存在了两种情况,第一种情况即不在一个集合里面这一种情况,第二种情况是在一个集合里面这种情况
1,让我们先来看下第一种情况,不在一个集合里面的合并操作的relation传递公式如何推导
在这个博客里面 https://blog.csdn.net/niushuai666/article/details/6981689
我看到了一种用向量来表达的操作
假设我们知道1<-2的关系 4<-3的关系 2->3的关系
那么向量4->1是我们要求的关系
可得4->1=1->2+2->3+3->4
即1->2的关系可以由2->1推导得到 捕食者与被被捕食者的关系是相对的
若1被2捕食 即1到2的路径的权值为1
那么2捕食1,即2到1的路径的权值为2
所以可得转换公式(3-单向路径权值)%3 (注:后面的表达式参考第二个图)
即可得1->2 (3-data[a].relation)
2->3为(d-1) (d-1)
3->4为已知的边 (data[b].relation)
可得data[rootb].relation=(3-data[a].relation+(d-1)+(data[b].relation))%3
///我程序里是这样写的,因为代表的方向不同所以得到的表达式不一样本质上是一样的都是同一种方法推导出来的
///math[rooty].relation=(3+(d-1)+math[a].relation-math[b].relation)%3;
2,我们再来看下第二种情况,在一个集合里面,如何判断是否合理,
如图
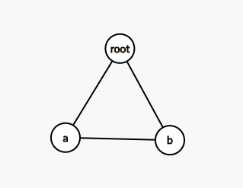
我们应该判断新加的边a-b是否合理,通过上面的查找压缩路径操作,我们可以得知,a与root的关系,b与root的关系
依旧用向量方法来判断,
a->root b->root已知
求a->b
那么a->b=a->root-b->root
按照上方简述的相对关系可得
a->b=a->root+root->b
即d-1=data[a].relation+(3-data[b].relation)%3;
即d-1=(data[a].relation-data[b].relation+3)%3
就可以判断多加的这条边是否符合条件了
附上代码
/** rid: 201353 user: 136155330 time: 2018-07-31 11:30:15 result: Accepted */ #include<iostream> #include<cstdio> #include<cstring> using namespace std; const int MAXN = 50005; int n,k,d,x,y; int sum;///统计错误的出现 typedef struct NODE { int parents; int relation; } node; node math[MAXN]; int acfind(int x)///寻找父节点 { int temp; if(math[x].parents==x) return x; /** 以下为压缩路径,首先我们可以证明得到 子节点到爷爷节点的关系,可以通过子节点到 父亲的关系,父亲节点到爷爷节点的关系得到 ,可得math[x].relation=(math[x].relation+math[temp].relation)%3 **/ temp=math[x].parents; math[x].parents=acfind(temp); math[x].relation=(math[x].relation+math[temp].relation)%3; return math[x].parents; } void Init() { sum=0; for(int i=0; i<MAXN; i++) { math[i].parents=i; math[i].relation=0;///0代表同类 } } void join(int a,int b) { int rootx,rooty; rootx=acfind(a); rooty=acfind(b); if(rootx!=rooty)///不在一个集合里,应该合并 ///应该求rooty->rootx { math[rooty].parents=rootx;///即将rooty连接到rootx math[rooty].relation=(3+(d-1)+math[a].relation-math[b].relation)%3; ///可以通过向量关系得到,math[rooty].relation } else///不在一个集合里 { if(d==1&&math[a].relation!=math[b].relation) { sum++; return ; } if(d==2&&((3-math[a].relation+math[b].relation)%3!=(d-1))) { sum++; return ; } } } int main() { scanf("%d%d",&n,&k); Init(); for(int i=0; i<k; i++) { scanf("%d%d%d",&d,&x,&y); if(x>n||y>n) { sum++; continue; } if(d==2&&x==y) { sum++; continue; } join(x,y); } printf("%d ",sum); return 0; }
附上拓展域的写法:
拓展域真香
#include <bits/stdc++.h> using namespace std; /** 食物链本题以前写过边带权 所以写一下拓展域,拓展域真香 存在三个域 同类域 捕食域 天敌域 similar predation enemy 那么假设是同类 那么similar predation enemy 相互连接 假设x 吃 y Merge x.predation y.similar Merge x.enemy y.predation Merge y.enemy x.similar 如果说是同类的话,那么连接的时候先判断Get(x.enemy) == Get(y.similar) || Get(x.predation) == Get(y.similar) || Get(y.enemy) == Get(x.similar) || Get(y.enemy) == Get(x.similar) 如果说是捕食的话,那么连接的时候先判断Get(x.similar) == Get(y.similar) || Get(x.enemy) == Get(y.similar) || Get(y.predation) == Get(x.similar) **/ const int MAXN = 50000 * 3 + 100; int pre[MAXN]; void Init() { for(int i = 0; i < MAXN; i ++) pre[i] = i; } int Get(int x) { return x == pre[x] ? x : pre[x] = Get(pre[x]); } void Merge(int x, int y) { int a = Get(x); int b = Get(y); if(a != b) pre[a] = b; } int n, k; int main() { scanf("%d%d", &n, &k); Init(); int wa = 0; for(int i = 0; i < k; i ++) { int d, x, y; scanf("%d%d%d", &d, &x, &y); if(x > n || y > n) { wa ++; continue; } if(x == y && d == 2) { wa ++; continue; } int x_sim = x; int y_sim = y; int x_pre = x + n; int y_pre = y + n; int x_ene = x + 2 * n; int y_ene = y + 2 * n; if(d == 1) { if(Get(x_pre) == Get(y_sim) || Get(x_ene) == Get(y_sim) || Get(y_pre) == Get(x_sim) || Get(y_ene) == Get(x_sim)) { wa ++; continue; } Merge(x_sim, y_sim); Merge(x_pre, y_pre); Merge(x_ene, y_ene); } else if(d == 2) { if(Get(x_sim) == Get(y_sim) || Get(x_ene) == Get(y_sim) || Get(y_pre) == Get(x_sim)) { wa ++; continue; } Merge(x_pre, y_sim); Merge(x_sim, y_ene); Merge(x_ene, y_pre); } } printf("%d ", wa); return 0; }