传送门:https://vjudge.net/contest/374932#problem/C
题意
有n个小孩围成一个圈,老师给第一第二个人,再隔一个人给第四个,再隔两个给第7个,以此类推。老师有无限的糖果问n个人是否都能get到糖果。
思路
这题只有我们模拟打表,很容易看出来结论是:n是2的幂则可以,不是则不行。那为什么是这样呢?我们可以推一下。
我们将孩子从0开始编号,最后一个孩子为n-1号,我们可以把派糖果看成是一个modn意义下的过程。
考虑第i颗糖果派给了f(i)号孩子,可以得到f(1)=0,f(2)=1,f(3)=3,f(4)=6,很明显这是一个差值在增大的数列,即为0 1 2 3...n-1的前n项和,我们很容易得到f(i)=(i-1)*i/2。
考虑f(i)和f(i+n),容易得出在modn体系下这两项是相等的,也就是说第i颗糖果和第i+n颗糖果派给的孩子是一样的。也就是说我们考虑只派n颗糖果的情况就行,在派n颗糖果的时候,如果有两颗糖果派给了同一个人,那么就肯定至少有一个人没有糖果,所以ans=no。此时肯定有f(a)=f(b),即(a-1)*a/2=(b-1)*b/2 (modn)
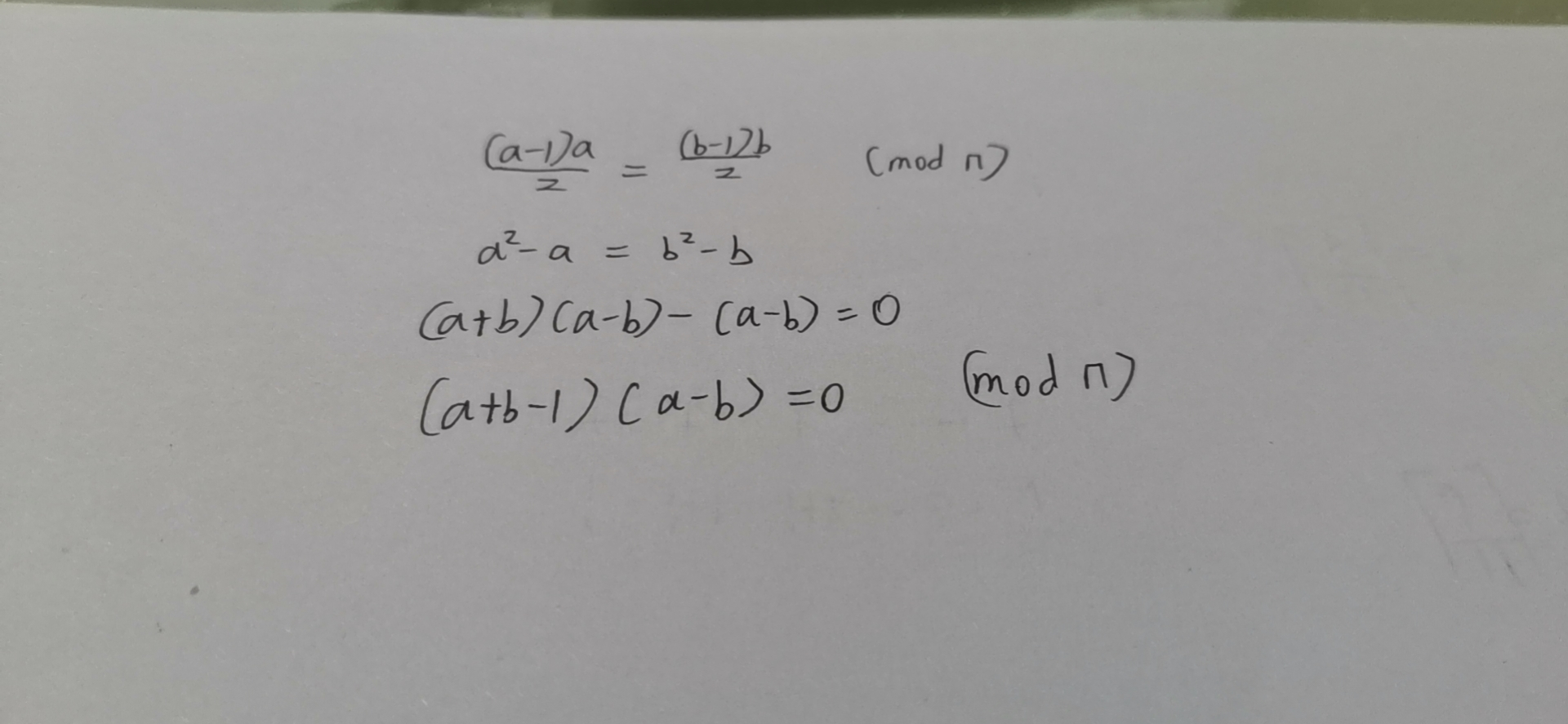
在modn意义下(a+b-1)(a-b)=0,意味着(a+b-1)(a-b)=k*n,又因为a和b是1到n的,所以k一定等于1,即(a+b-1)(a-b)=n。
我们可以观察这两个括号,无论ab是奇数还是偶数,两个括号的奇偶性一定不同。奇偶性不同意味着n如果不是2的幂一定不满足这个式子。证明可看这篇博客https://blog.csdn.net/scorpiocj/article/details/6267925