贪心算法

贪心算法

　　贪心算法(Greedy Algorithm)，是指在对问题求解时，总是做出在当前看来是最好的选择。也就是它所做出的仅是在某种意义上的局部最优解。

贪心算法的基本思路

1. 建立数学模型来描述问题。
   2. 把求解的问题分成若干个子问题。
      3. 对每一子问题求解，得到子问题的局部最优解。
         4. 把子问题的解局部最优解合成原来解问题的一个解。

贪心算法适用的问题

　　贪心策略适用的前提是：局部最优策略能导致产生全局最优解。也就是当算法终止时，局部最优等于全局最优。

贪心算法的实现框架

从问题的某一初始解出发；
while （能朝给定总目标前进一步）
{
利用可行的决策，求出可行解的一个解元素；
}
由所有解元素组合成问题的一个可行解；

一个简单的例子

纸币找零问题

​ 假设1元、2元、5元、10元、20元、50元、100元的纸币，张数不限制，现在要用来支付K元，至少要多少张纸币？

package com.ks.greedy;

/**
 * @author 柯神_
 * @date 2021-01-04 18:28:23
 * @Description 贪心算法，经典例子
 */

public class GiveMoney {

    public static void main(String[] args) {
        greedyGiveMoney(251);
    }

    /**
     * 例子1：支付问题
     */
    public static void greedyGiveMoney(int money) {
        System.out.println("支付: " + money + "元");
        int[] moneyLevel = {1, 5, 10, 20, 50, 100};
        int count = 0;
        for (int i = moneyLevel.length - 1; i >= 0; i--) {
            int num = money / moneyLevel[i];
            int mod = money % moneyLevel[i];
            money = mod;
            count += num;
            if (num > 0) {
                System.out.println("需要" + num + "张" + moneyLevel[i] + "块的");
            }
        }
        System.out.println("需要纸币" + count + "张");
    }
}

结果演示

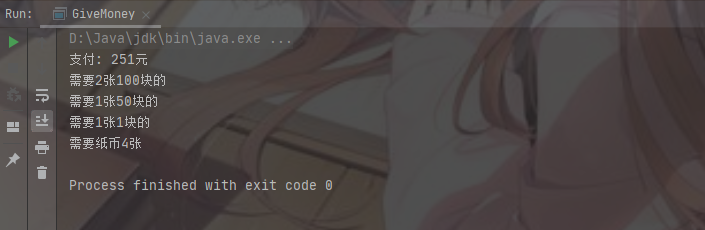
一个力扣上的简单例子

买股票的最佳时期

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:

输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

贪心算法：一句话 —— 所有的上升线段都计算进去

package com.ks.greedy;

/**
 * @author 柯神_
 * @date 2021-01-04 22:30:09
 * @Description 贪心算法：买股票的最佳时期
 */
public class BuyShares {

  public static void main(String[] args) {
    int[] x = {1, 2, 3, 4, 1, 2};
    System.out.println(buyShares(x));
  }


  public static int buyShares(int[] price) {
    int n = price.length;

    if (n < 2) return 0;

    int res = 0;
    for (int i = 1; i < n; i++) {
      res += Math.max(price[i] - price[i - 1], 0);
    }
    return res;
  }
}

结果演示