1.在c#中创建一个委托类型的时候,需要使用关键字delegate,当c#处理一个委托类型时,会产生一个派生自System.MulticastDelegate的密封类,这个类与基类System.Delegate一起为委托提供必要的基础设施,例如委托public delegate int BinaryOp(int x,int y);生成以下类:
sealed class BinaryOp:System.MulticastDelegate
{
public int Invoke(int x,int y);
public IAsyncResult BeginInvoke(int x,int y,AsyncCallBack cb,object state);
public int EndInvoke(IAsyncResult result);
}
Invoke方法定义的参数和返回值完全匹配BinaryOp委托的定义,BeginInvoke前两个参数也是基于委托,后两个参数用于异步方法调用,EndInvoke方法的返回值与委托相同,总是以一个实现了IAsyncResult 接口的对象作为其唯一的参数。若委托的参数中包含ref或out类型,则EndInvoke方法里也会新增相应的参数。
2.委托实例
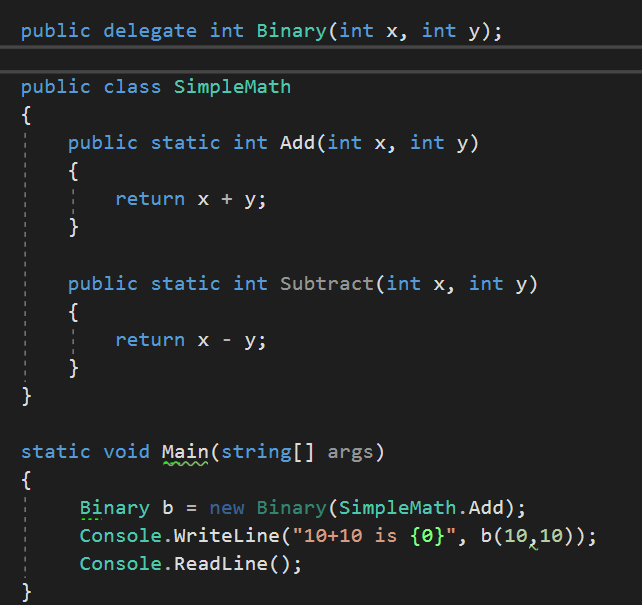
创建一个SimpleMath的类,其中定义了两个静态方法,如果要将目标对象方法插入委托对象,只要向委托的构造函数传入方法名称,.Net 委托是安全的,如果将一个不匹配的方法传入委托,则会收到编译器错误。
3.委托对象

通过迭代由GetInvocationList()返回System.Delegate数组,调用每个对象的Target(表示委托维护的静态方法的信息)和Method(表示委托维护的对象信息)属性,此时Method为Int32 Add(Int32,Int32),Target为空,这是由于委托指向的是静态方法,没有对象被引用。此时如果去掉方法的静态属性,通过对象来调用,Target则不为空,显示对象信息。
4.使用委托发送对象状态通知

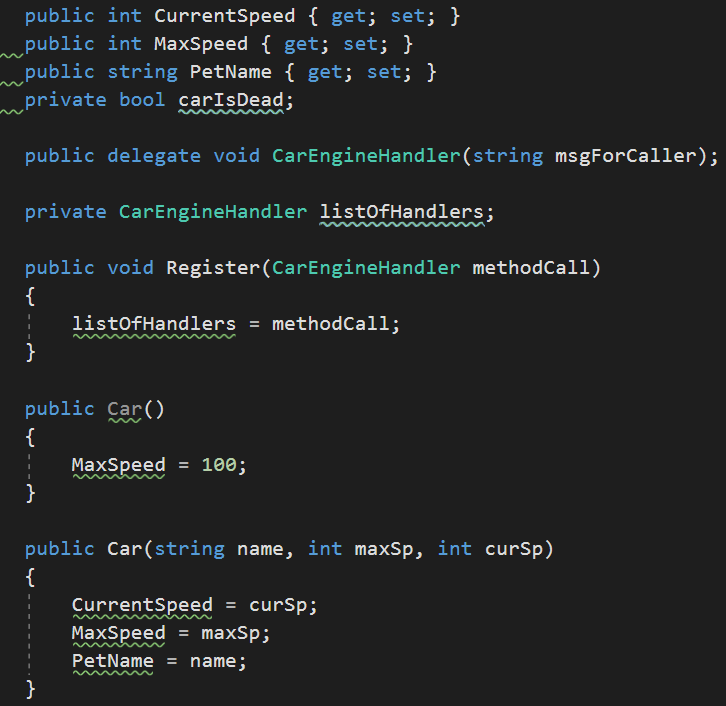

5.支持多路广播
一个委托对象可以维护一个可调用方法的列表,而不只是一个方法。给一个委托对象添加方法时,直接重载+=操作符,使用该操作符时,编译器会转换为静态Delegate.Combine()的调用。
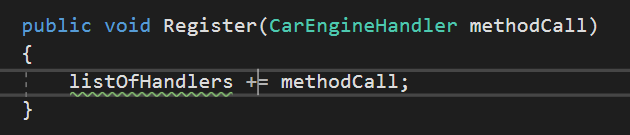
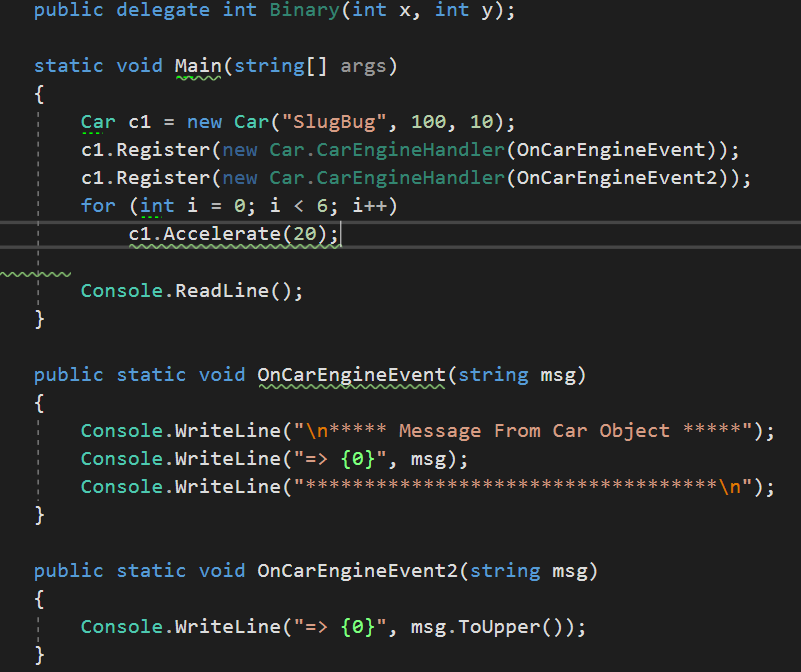
6.从委托的调用列表中移除成员
Delegate还定义了一个静态Remove方法,可以从委托对象的调用列表中移除方法,-=为简写方式。
7.方法组转换语法
如果要调用Delegate中继承的任何成员,手工创建一个委托变量是直接的方式,但多数情况不需要依靠委托对象,委托对象只是为了传递作为构造函数参数的方法名称。c#允许我们直接提供方法的名称,此时c#仍然能够检验类型安全。
8.泛型委托
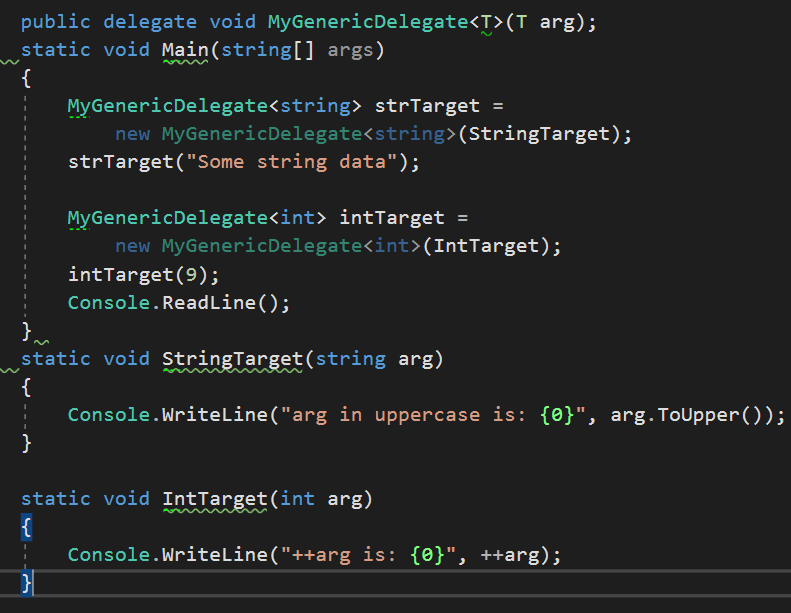
9.如果我们只需要一组参数并返回一个值(或void)的委托,委托名没有任何意义,可以使用Action<>或Fun<>委托。泛型Action<>委托定义在mscorlib.dll和System.Core.dll中的System命名空间,可以指向多至16个参数。
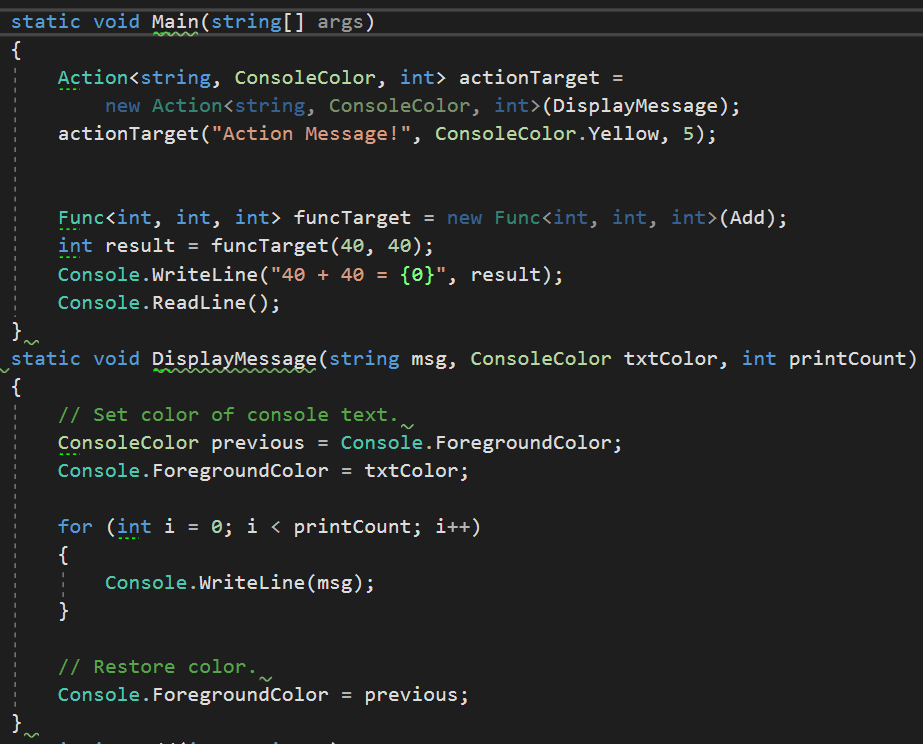
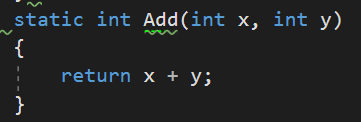
10.Event关键字
为了简化自定义方法的构建来为委托调用列表增加和删除方法,c#提供了关键字Event,会自动提供注册和注销方法以及任何必要的委托类型成员变量,为私有的,不能直接从触发事件的对象去访问。
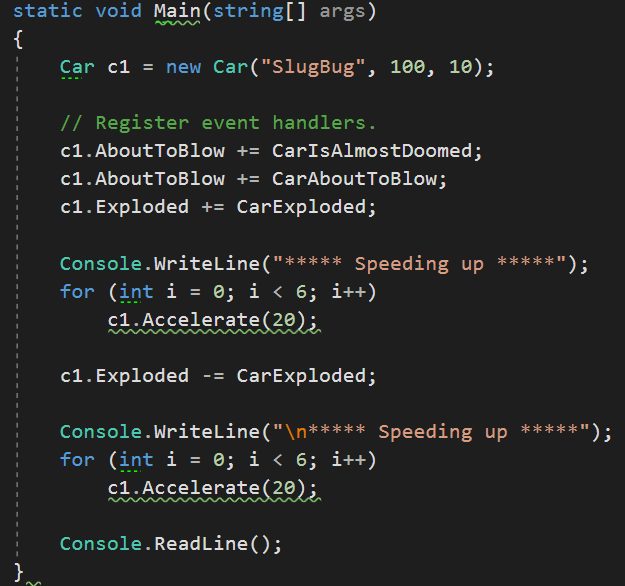

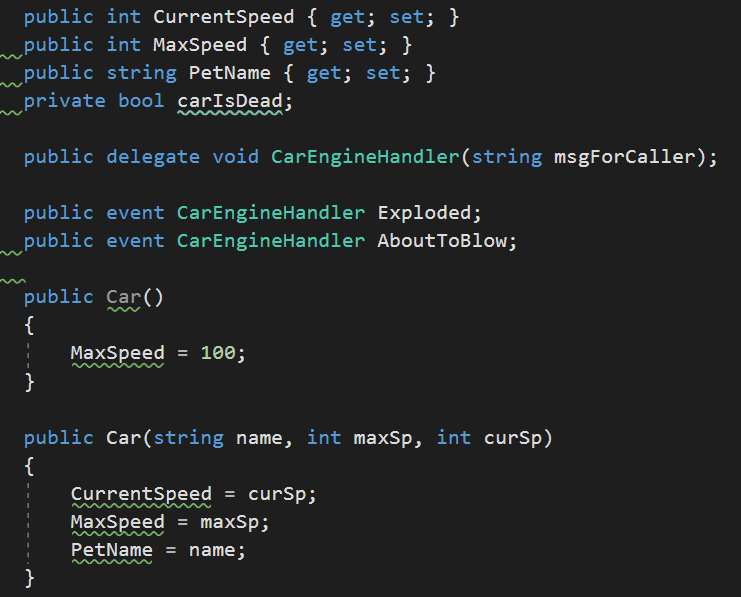
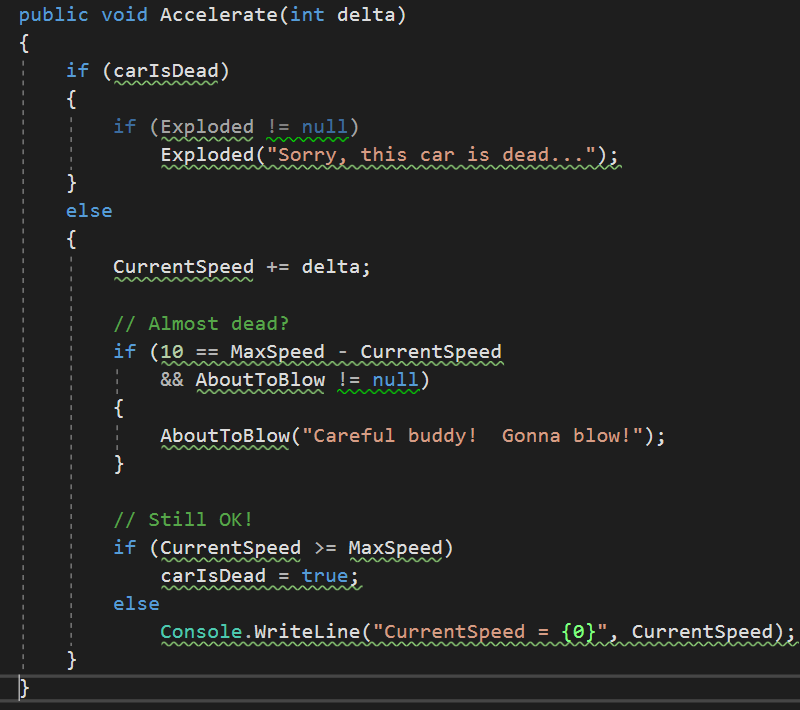
11.创建自定义的事件参数
查看某个事件时发现,底层委托的第一个参数为System.Object,第二个参数派生自System.EventArgs,第一个表示对发送事件对象的引用,第二个表示相关信息,System.EventArgs表示不发送任何自定义信息的事件,如果要发送信息,则可以构建一个派生自System.EventArgs的类:
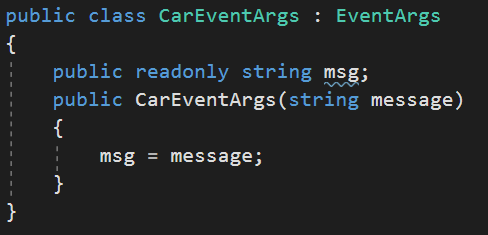
此时委托为 public delegate void CarEngineHandler(object sender, CarEventArgs e);


12.泛型EventHandler<T>委托
可以用EventHandler<CarEventArgs>替代CarEngineHandler。