一.基于度量的程序结构分析
在进行分析之前,先解释一下以下几个缩写:
LOC:代码行数
CC:圈复杂度,反映了程序中if/while等判定条件的数量,越高意味着代码越可能质量低且难以测试、维护。
PC:方法参数个数
NOF:类的属性个数
NOPF:类的public属性个数
NOM:类的方法个数
NOPM:类的public方法个数
NC:类的子类个数
DIT:类的继承树深度
LCOM:类中内聚度的缺乏,越大意味着内聚度越差。
FAN-OUT:某个类引用其他类的次数
FAN-IN:类被其他类引用的次数
1、第一次作业
(1)设计思路
第一次作业使用了两个类:PolyItem用于管理多项式的每一项;PolyDerivation通过调用PolyItem类实现多项式合法性判定以及求导。在判断输入表达式合法性的同时,运用arraylist结构构造了一个每一项为PolyItem类的动态链表,对这个链表进行求导,最终得到多项式的导数,由于每一个PolyItem类维护系数和指数两个属性,因此在合并同类项的过程中可以通过判断指数是否相等而进行合并。
(2)结构分析
类图如下所示:
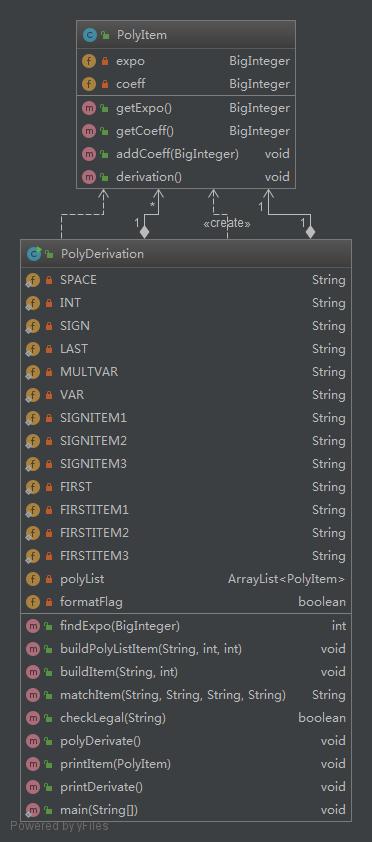
可见,PolyItem仅包含了对某一项求导、合并同类项的简单方法,而PolyDerivation则比较冗长的包含了多种处理。程序度量如下:
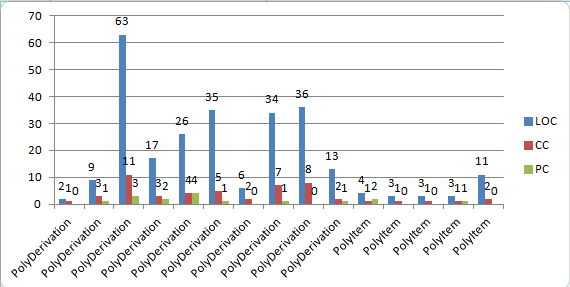
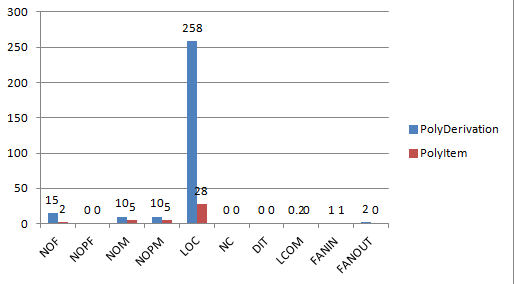
显然,与PolyDerivation相比,PolyItem中的方法行数少、复杂度低,比较容易测试,而PolyDerivation中方法CC有的高达11,这给程序的测试带来了一定困难。此外,PolyDerivation类的代码长度过长,达258行,表明类中可能存在比较多的冗余代码。由于第一次作业写的时候刚刚接触JAVA,基本是按照C的套路写的,类的划分并不好,也并没有用到继承(当时也并不知道继承是啥),因此程序层次并不深,却也导致了类中的内聚度比较好(大概是因为写成了C吧)。
2、第二次作业
(1)设计思路
第二次作业使用了三个类:PolyItem与第一次作业类似,用于管理多项式的某一项;PolyDerivation也与第一次作业的作用一致,用于识别整个多项式并完成求导;新增的Derivation类用于单独处理求导、合并同类项操作,目的是将不同类别因子的求导方法与多项式类分离。第二次作业的思路与第一次作业没有太大的区别,仅仅是在PolyItem类中多维护了sin(x)、cos(x)的系数这两个属性,合并同类项的方式也比较类似。
(2)结构分析
类图如下:

每个类及类中方法的度量如下:
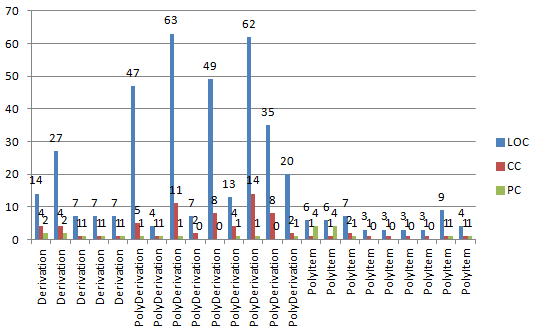
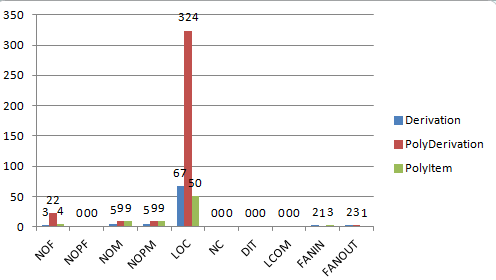
可见,仍旧是多项式类的代码行数、方法行数、属性个数、复杂度比较高,其余两个类则比较简洁。由于求导类仅用于处理每一项的求导,项类则只用于管理合并同类项等粒度到项的操作,类内的内聚度比较好(由LCOM值较低可得),类间的耦合度较少。但是在第二次作业的时候,我显然没有领会到老师所提的代码重构的真正意图,我的这种架构在遇到第三次作业的之后完全崩溃,这告诉我代码的可扩展性也是很重要的,虽然在一开始设计时,我往往更关注本次作业所要完成的任务,而忽略了如何支撑更多、更复杂的功能。
3. 第三次作业
(1)设计思路
第三次作业明显比前两次难了很多,由于前两次作业我都没有考虑支持嵌套的问题,也没有使用继承、接口,我进行了完全的重构。如果说第二次作业是在第一次作业的基础上进行了扩展的话,第三次作业则是完完全全的重写。这次作业不仅在处理嵌套问题上难住了我,在最开始的多项式识别阶段就令我感到头疼。因为正则表达式不能支持递归识别,我最终采用了类似编译器的递归下降子程序处理方法,并在识别的过程中显式构造了一棵表达式树,这棵表达式树的叶子节点是形如x^2、sin(x)^2、cos(x)^2、常数这样的基本因子,树的中间节点是加、减、乘、嵌套等运算,由于在嵌套函数f(g(x))的求导过程中,sin(x)^2与sin(factor)^2的求导方式没有本质的区别,因此,我将其合并成了同一类。表达式树上的每一类结点都维护一个属于自己的求导方式,树建立之后,通过调用根节点的求导方法即实现整个表达式的求导。
(2)结构分析
这次涉及的类比较多,类图如下所示:
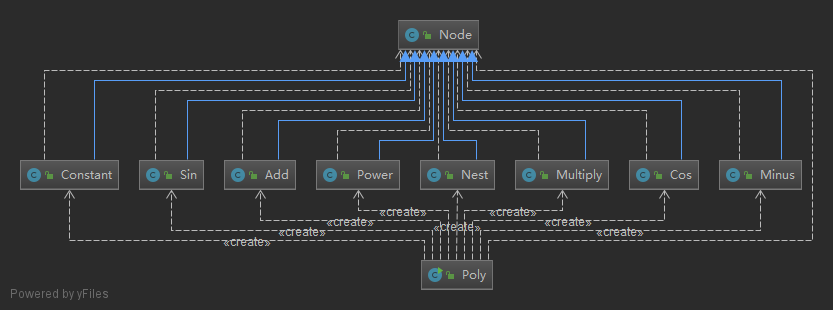




类的度量如下:

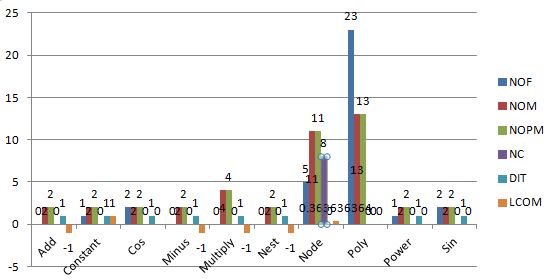
可见,使用继承之后,类的属性和方法有了明显的减少,但是有的类里出现了内聚度降低的情况,这表明类的划分并没有符合高内聚低耦合的原则。尽管使用了继承,但是继承树的层次相对比较小,大多为1层,结构比较简单。尽管第三次作业的架构难以实现优化的目标,但是通过将求导这个大问题拆成不同形式求导的小问题,简化了程序的结构,只要独立地思考每个类所要完成的功能,再最后进行简单的组装,就能实现求导功能。在这里,想简要的说明一下第三次作业中我关于优化的设计,因为并没有从整体上考虑优化的问题,我仅仅是在求导过程中进行了比较细节的优化,例如:在形如x^2这样的基本函数的求导过程中,如果系数是1,则直接得到x而非x^1;在加、减、乘、嵌套的求导时,如果乘法的因子中包含0,则直接得到0,而不进行额外的运算,如果涉及的各因子、项都是常数,则可以直接运算的到结果而不需要表达式输出等。尽管这些优化效果可能不是特别显著,但也起到了一定的作用。
二.程序中的bug分析
这三次作业中,前两次作业的设计都比较简单,主要的思想是在判断多项式合法性的过程中,构造了由项类组成的动态链表,再进行求导、合并同类项以达到优化的目的。第三次作业则采用了树的结构,在判断多项式合法性的过程中构造一棵表达式树,通过对根节点求导得到整个表达式的导数,并在每个类所维护的求导方法中进行力所能及的优化。显然,表达式树的结构要更具有可扩展性,并且能支持嵌套结构,且在实现的过程中,类之间的耦合度更低,只要实现好每个子类的求导,再将树构建好,即可完成整个表达式的求导。
由于表达式树的构建相对复杂一点,也比较容易产生bug。在构建的过程中,我主要遇到的是有关“不加括号导致运算顺序出错”的问题。在中间结点的求导过程中,由于左右两棵子树可能是因子、项、表达式中的任意一种,因此需要额外注意加括号的问题。例如:(sin(x) - x*cos(x))' = cos(x) - (cos(x) - x*sin(x)),如果不加括号,就会产生运算错误。
- 在减法求导过程中,(f(x)-g(x))' = f'(x) - g'(x),为保证运算的正确性,减号右边需要加括号。
- 乘法求导时,(f(x)*g(x))' = f'(x)*g(x) + f(x)*g'(x),由于项的性质,f(x)与g(x)无需加括号,但是f'(x)和g'(x)可能出现“一项变两项”的情况,因此,需要加括号。
- 嵌套求导,f'(g(x)) = f'(g(x)) * g'(x),由于外层的f(x)函数是基本因子的形式,求导后不需要加括号,但是g(x)求导后可能出现“一项变两项”的情况,也需要加括号。
三.使用对象创建模式
第三次作业中,我应用的主要是继承,先构建一个基本的树节点,其中维护左右子树结点等属性以及求导、获取子树导数值等方法,而其子类则是通过重写求导方法实现不同函数求导的功能。在了解了工厂模式的相关内容之后,我将第三次作业进行了重构。
重构之后的类图大致为:
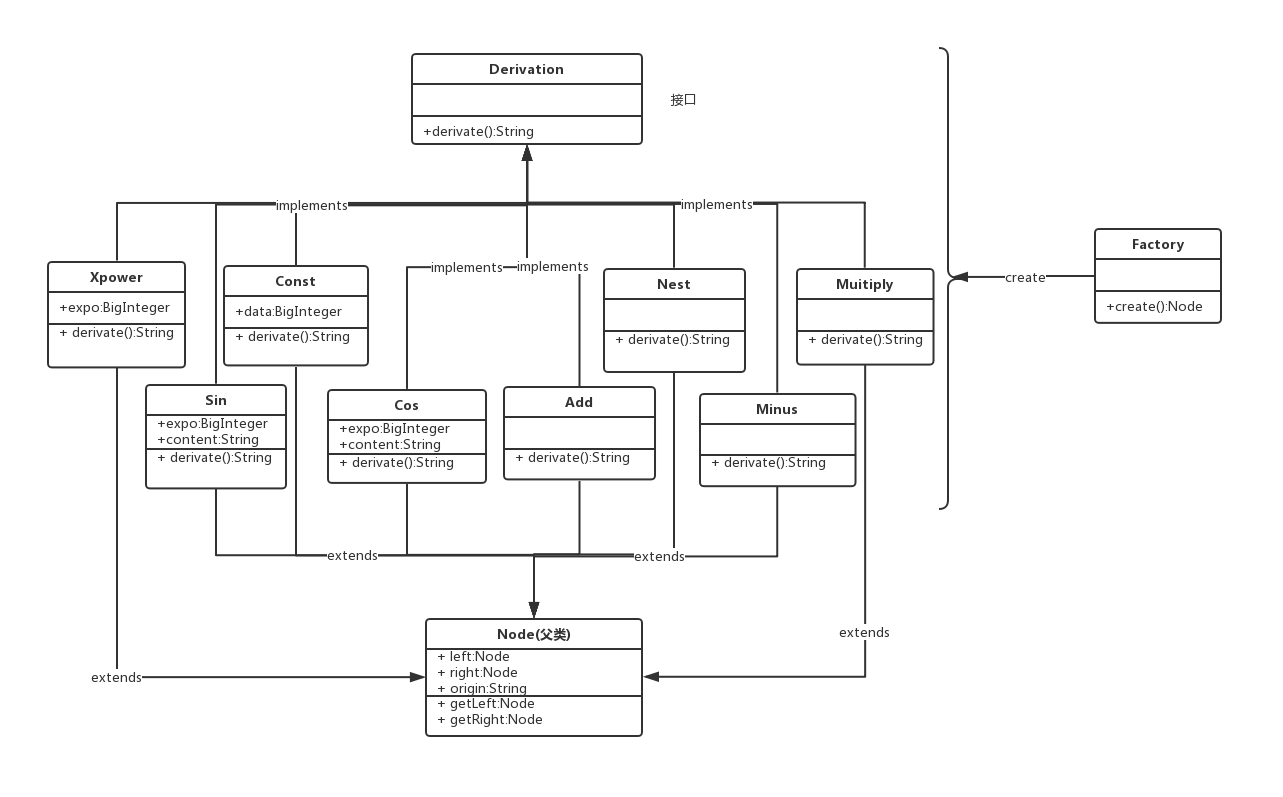
使用工厂模式可以很方便地根据需求创建不同类型的结点,并以求导函数为接口,实现不同类型函数的求导。
四. 总结
这三次递进式的求导作业让我经历了“如何写JAVA”->“如何尽量写出不像C的JAVA”的过程,每次需求的增加不仅考验我们需求分析的能力,也考验了我们设计的能力。在写代码之前,先做好设计是很有用的,这不仅可以防止出现边写边改的情况,也有助于后期debug阶段更迅速定位bug。