zoukankan      html  css  js  c++  java

  • （FFT）HDU 6088（2017 多校第5场 1004）Rikka with Rock-paper-scissors

    Rikka with Rock-paper-scissors

    As we know, Rikka is poor at math. Yuta is worrying about this situation, so he gives Rikka some math tasks to practice. There is one of them: 

    Alice and Bob are going to play a famous game: Rock-paper-scissors. Both of them don’t like to think a lot, so both of them will use the random strategy: choose rock/paper/scissors in equal probability. 

    They want to play this game nn times, then they will calculate the score ss in the following way: if Alice wins aa times, Bob wins bb times, and in the remaining n−a−bn−a−b games they make a tie, the score will be the greatest common divisor of aaand bb. 

    Know Yuta wants to know the expected value of s×32ns×32n. It is easy to find that the answer must be an integer. 

    It is too difficult for Rikka. Can you help her? 

    Note: If one of a,ba,b is 00, we define the greatest common divisor of aa and bb as a+ba+b.

    InputThe first line contains a number t(1≤t≤20)t(1≤t≤20), the number of the testcases. There are no more than 22 testcases with n≥104n≥104. 

    For each testcase, the first line contains two numbers n,mo(1≤n≤105,108≤mo≤109)n,mo(1≤n≤105,108≤mo≤109) 

    It is guaranteed that momo is a prime number.    OutputFor each testcase, print a single line with a single number -- the answer modulo momo.Sample Input

    5
1 998244353
2 998244353
3 998244353
4 998244353
5 998244353

    Sample Output

    6
90
972
9720
89910

    理解题意后很容易可以列出官方题解中的第一个式子。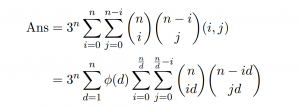

    化到第二个式子需要用到莫比乌斯反演（这里用莫比乌斯反演证明的内容其实是欧拉函数的一个常用性质）

    这样我们就成功化出了官方题解中的式子，接下来只需要枚举d，用FFT加速计算后项的结果即可。

    （详细代码晚上再补上）

     8.11UPD:

    时隔好几天，才终于把这个题过了……这个题貌似非常卡常，加上自己本来NTT、FFT就菜，反反复复用不同方法写了4遍，最后用MYY的集训队论文中的方法才终于AC……

    在此贴上两种代码吧，分别是NTT三模数会TLE的代码，和套MYY模版的优化版FFT能AC的代码。

    NTT三模数版：

    　　

      1 #include <cstdio>
  2 #include <iostream>
  3 #include <algorithm>
  4 #include <vector>
  5 #include <set>
  6 #include <map>
  7 #include <string>
  8 #include <cstring>
  9 #include <stack>
 10 #include <queue>
 11 #include <cmath>
 12 #include <ctime>
 13 #include<bitset>
 14 #include <utility>
 15 using namespace std;
 16 #define REP(I,N) for (I=0;I<N;I++)
 17 #define rREP(I,N) for (I=N-1;I>=0;I--)
 18 #define rep(I,S,N) for (I=S;I<N;I++)
 19 #define rrep(I,S,N) for (I=N-1;I>=S;I--)
 20 #define FOR(I,S,N) for (I=S;I<=N;I++)
 21 #define rFOR(I,S,N) for (I=N;I>=S;I--)
 22 #define rank rankk
 23 #define DFT FFT
 24 typedef unsigned long long ull;
 25 typedef long long ll;
 26 const int INF=0x3f3f3f3f;
 27 const ll INFF=0x3f3f3f3f3f3f3f3fll;
 28 //const ll M=1e9+7;
 29 const ll maxn=2e5+7;
 30 const int MAXN=1005;
 31 const int MAX=1e6+5;
 32 const int MAX_N=MAX;
 33 const ll MOD=1e9+7;
 34 //const double eps=0.00000001;
 35 //ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
 36 template<typename T>inline T abs(T a) {return a>0?a:-a;}
 37 inline ll powMM(ll a,ll b,ll M){
 38     ll ret=1;
 39     a%=M;
 40 //    b%=M;
 41     while (b){
 42         if (b&1) ret=ret*a%M;
 43         b>>=1;
 44         a=a*a%M;
 45     }
 46     return ret;
 47 }
 48 void open()
 49 {
 50     freopen("1004.in","r",stdin);
 51     freopen("out.txt","w",stdout);
 52 }
 53 inline ll mul(ll a,ll b,ll p){
 54   a%=p; b%=p;
 55   return ((a*b-(ll)((ll)((long double)a/p*b+1e-3)*p))%p+p)%p;
 56 }
 57 ll euler[maxn+5];
 58 void getEuler()
 59 {
 60     memset(euler,0,sizeof(euler));
 61     euler[1] = 1;
 62     for(int i = 2;i <= (int)1e5;i++)
 63         if(!euler[i])
 64         for(int j = i;j <= (int)1e5; j += i)
 65         {
 66             if(!euler[j]) euler[j] = j;
 67             euler[j] = euler[j]/i*(i-1);
 68         }
 69 }
 70 
 71 /*NTT部分*/
 72 //const int N = 1 << 18;
 73 const int NUM = 20;
 74 ll  wn[5][NUM];
 75 ll P[5]={469762049,998244353,1004535809};
 76 ll fac[maxn],inv[maxn];
 77 ll G=3;
 78 ll A[3][maxn<<1],B[maxn<<1];
 79 ll quick_mod(ll a, ll b, ll m)
 80 {
 81     ll ans = 1;
 82     a %= m;
 83     while(b)
 84     {
 85         if(b & 1)
 86         {
 87             ans = ans * a % m;
 88             b--;
 89         }
 90         b >>= 1;
 91         a = a * a % m;
 92     }
 93     return ans;
 94 }
 95 void GetWn(int id)//预处理原根的幂次
 96 {
 97     for(int i = 0; i < NUM; i++)
 98     {
 99         int t = 1 << i;
100         wn[id][i] = quick_mod(G, (P[id] - 1) / t, P[id]);
101     }
102 }
103 void Rader(ll a[], int len)
104 {
105     int j = len >> 1;
106     for(int i = 1; i < len - 1; i++)
107     {
108         if(i < j) swap(a[i], a[j]);
109         int k = len >> 1;
110         while(j >= k)
111         {
112             j -= k;
113             k >>= 1;
114         }
115         if(j < k) j += k;
116     }
117 }
118 void NTT(ll a[], int len, int ids,int on=1)//NTT的数组 下标从0开始 数组长度len
119 {
120     Rader(a, len);
121     int id = 0;
122     for(int h = 2; h <= len; h <<= 1)
123     {
124         id++;
125         for(int j = 0; j < len; j += h)
126         {
127             ll w = 1;
128             for(int k = j; k < j + h / 2; k++)
129             {
130                 ll u = a[k] % P[ids];
131                 ll t = w * a[k + h / 2] % P[ids];
132                 a[k] = (u + t) % P[ids];
133                 a[k + h / 2] = (u - t + P[ids]) % P[ids];
134                 w = w * wn[ids][id] % P[ids];
135             }
136         }
137     }
138     if(on == -1)
139     {
140         for(int i = 1; i < len / 2; i++)
141             swap(a[i], a[len - i]);
142         ll inv = quick_mod(len, P[ids] - 2, P[ids]);
143         for(int i = 0; i < len; i++)
144             a[i] = a[i] * inv % P[ids];
145     }
146 }
147 int t;
148 int n;
149 ll mo,an;
150 ll crt(ll x,ll y,ll z)
151 {
152     ll M=P[0]*P[1];
153     ll inv1=quick_mod(P[0]%P[1],P[1]-2LL,P[1]),inv2=quick_mod(P[1]%P[0],P[0]-2LL,P[0]),inv12=quick_mod(M%P[2],P[2]-2LL,P[2]);
154     ll re=(mul(x*P[1]%M,inv2,M)+mul(y*P[0]%M,inv1,M))%M;
155     ll k=(z+P[2]-re%P[2])%P[2]*inv12%P[2];
156     return (k*(M%mo)%mo+re)%mo;
157 }
158 int main()
159 {
160     for(int i=0;i<3;i++)
161         GetWn(i);
162     getEuler();
163     scanf("%d",&t);
164     while(t--)
165     {
166         scanf("%d%lld",&n,&mo);
167         P[3]=mo;
168         fac[0]=1LL;
169         for(int j=1;j<=n;j++)
170             fac[j]=fac[j-1]*(ll)j%mo;
171         inv[n]=quick_mod(fac[n],mo-2,mo);
172         for(int j=n-1;j>=0;j--)
173             inv[j]=(ll)(j+1LL)*inv[j+1]%mo;
174         an=0;
175         for(int g=1;g<=n;g++)
176         {
177             int ge=n/g;
178             ll temhe=0;
179             if(ge<2)
180                 break;
181             memset(A,0,sizeof(A));
182             int length=0;
183             while((1<<length)<2*ge)
184                 ++length;
185             for(int j=0;j<3;j++)
186             {
187                 memset(B,0,sizeof(B));
188                 for(int i=0;i<=ge-2;i++)
189                     A[j][i]=B[i]=inv[(i+1)*g];
190                 NTT(A[j],1<<length,j);NTT(B,1<<length,j);
191                 for(int i=0;i<(1<<length);i++)
192                     A[j][i]=A[j][i]*B[i]%P[j];
193                 NTT(A[j],1<<length,j,-1);
194             }
195             for(int i=0;i<=ge-2;i++)
196             {
197                 temhe=(temhe+mul(crt(A[0][i],A[1][i],A[2][i]),inv[n-(i+2)*g],mo))%mo;
198             }
199                 temhe=mul(temhe,fac[n],mo);
200                 an=(an+mul(temhe,(ll)euler[g],mo))%mo;
201             }
202             an=(an+(ll)n*powMM(2LL,(ll)n,mo)%mo)%mo;
203             an=an*powMM(3LL,(ll)n,mo)%mo;
204             printf("%lld
",an);
205     }
206     return 0;
207 }

    MYY优化FFT版

      1 #include <bits/stdc++.h>
  2 
  3 using namespace std;
  4 
  5 #define REP(i, a, b) for (int i = (a), _end_ = (b); i < _end_; ++i)
  6 #define debug(...) fprintf(stderr, __VA_ARGS__)
  7 #define mp make_pair
  8 #define x first
  9 #define y second
 10 #define pb push_back
 11 #define SZ(x) (int((x).size()))
 12 #define ALL(x) (x).begin(), (x).end()
 13 #define ll LL
 14 template<typename T> inline bool chkmin(T &a, const T &b) { return a > b ? a = b, 1 : 0; }
 15 template<typename T> inline bool chkmax(T &a, const T &b) { return a < b ? a = b, 1 : 0; }
 16 
 17 typedef long long LL;
 18 const int maxn=2e5+7;
 19 inline ll powMM(ll a,ll b,ll M){
 20     ll ret=1;
 21     a%=M;
 22 //    b%=M;
 23     while (b){
 24         if (b&1) ret=ret*a%M;
 25         b>>=1;
 26         a=a*a%M;
 27     }
 28     return ret;
 29 }
 30 ll euler[maxn+5];
 31 void getEuler()
 32 {
 33     memset(euler,0,sizeof(euler));
 34     euler[1] = 1;
 35     for(int i = 2;i <= (int)1e5;i++)
 36         if(!euler[i])
 37         for(int j = i;j <= (int)1e5; j += i)
 38         {
 39             if(!euler[j]) euler[j] = j;
 40             euler[j] = euler[j]/i*(i-1);
 41         }
 42 }
 43 const int oo = 0x3f3f3f3f;
 44 
 45 int Mod = 1e9 + 7;
 46 
 47 const int max0 = 262144;
 48 
 49 struct comp
 50 {
 51     double x, y;
 52 
 53     comp(): x(0), y(0) { }
 54     comp(const double &_x, const double &_y): x(_x), y(_y) { }
 55 
 56 };
 57 
 58 inline comp operator+(const comp &a, const comp &b) { return comp(a.x + b.x, a.y + b.y); }
 59 inline comp operator-(const comp &a, const comp &b) { return comp(a.x - b.x, a.y - b.y); }
 60 inline comp operator*(const comp &a, const comp &b) { return comp(a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x); }
 61 inline comp conj(const comp &a) { return comp(a.x, -a.y); }
 62 
 63 const double PI = acos(-1);
 64 
 65 int N, L;
 66 
 67 comp w[max0 + 5];
 68 int bitrev[max0 + 5];
 69 
 70 void fft(comp *a, const int &n)
 71 {
 72     REP(i, 0, n) if (i < bitrev[i]) swap(a[i], a[bitrev[i]]);
 73     for (int i = 2, lyc = n >> 1; i <= n; i <<= 1, lyc >>= 1)
 74         for (int j = 0; j < n; j += i)
 75         {
 76             comp *l = a + j, *r = a + j + (i >> 1), *p = w;
 77             REP(k, 0, i >> 1)
 78             {
 79                 comp tmp = *r * *p;
 80                 *r = *l - tmp, *l = *l + tmp;
 81                 ++l, ++r, p += lyc;
 82             }
 83         }
 84 }
 85 
 86 inline void fft_prepare()
 87 {
 88     REP(i, 0, N) bitrev[i] = bitrev[i >> 1] >> 1 | ((i & 1) << (L - 1));//FFT的01串
 89     REP(i, 0, N) w[i] = comp(cos(2 * PI * i / N), sin(2 * PI * i / N));
 90 }
 91 
 92 inline void conv(int *x, int *y, int *z)
 93 {
 94     REP(i, 0, N) (x[i] += Mod) %= Mod, (y[i] += Mod) %= Mod;
 95     static comp a[max0 + 5], b[max0 + 5];
 96     static comp dfta[max0 + 5], dftb[max0 + 5], dftc[max0 + 5], dftd[max0 + 5];
 97 
 98     REP(i, 0, N) a[i] = comp(x[i] & 32767, x[i] >> 15);
 99     REP(i, 0, N) b[i] = comp(y[i] & 32767, y[i] >> 15);
100     fft(a, N), fft(b, N);
101     REP(i, 0, N)
102     {
103         int j = (N - i) & (N - 1);
104         static comp da, db, dc, dd;
105         da = (a[i] + conj(a[j])) * comp(0.5, 0);
106         db = (a[i] - conj(a[j])) * comp(0, -0.5);
107         dc = (b[i] + conj(b[j])) * comp(0.5, 0);
108         dd = (b[i] - conj(b[j])) * comp(0, -0.5);
109         dfta[j] = da * dc;
110         dftb[j] = da * dd;
111         dftc[j] = db * dc;
112         dftd[j] = db * dd;
113     }
114     REP(i, 0, N) a[i] = dfta[i] + dftb[i] * comp(0, 1);
115     REP(i, 0, N) b[i] = dftc[i] + dftd[i] * comp(0, 1);
116     fft(a, N), fft(b, N);
117     REP(i, 0, N)
118     {
119         int da = (LL)(a[i].x / N + 0.5) % Mod;
120         int db = (LL)(a[i].y / N + 0.5) % Mod;
121         int dc = (LL)(b[i].x / N + 0.5) % Mod;
122         int dd = (LL)(b[i].y / N + 0.5) % Mod;
123         z[i] = (da + ((LL)(db + dc) << 15) + ((LL)dd << 30)) % Mod;
124     }
125 }
126 int t;
127 int fac[max0],inv[max0];
128 int an,num,n;
129 int A[max0],B[max0],C[max0];
130 int main()
131 {
132     getEuler();
133     scanf("%d",&t);
134     while(t--)
135     {
136         scanf("%d%d",&n,&Mod);
137         fac[0]=1;
138         for(int i=1;i<=n;i++)
139             fac[i]=1LL*i*fac[i-1]%Mod;
140         inv[n]=powMM(1LL*fac[n],Mod-2,Mod);
141         for(int i=n-1;i>=0;i--)
142             inv[i]=(ll)(i+1LL)*inv[i+1]%Mod;
143         an=num=0;
144         for(int g=1;g<=n;g++)
145         {
146             num=0;
147             int ge=n/g;
148             if(ge<2)
149                 break;
150             for(int i=0;i<=ge-2;i++)
151                 A[i]=B[i]=inv[(i+1)*g];
152             L=N=0;
153             for ( ; (1 << L) <2*ge; ++L);
154                 N = 1 << L;
155             for(int i=ge-1;i<(1<<L);i++)
156                 A[i]=B[i]=0;
157             fft_prepare();
158             conv(A,B,C);
159             for(int i=0;i<=ge-2;i++)
160                 num=(num+(ll)(C[i]+Mod)%Mod*inv[n-(i+2)*g]%Mod)%Mod;
161             num=(ll)num*fac[n]%Mod;
162             an=(an+(ll)num*euler[g]%Mod)%Mod;
163         }
164         an=(an+(ll)n*powMM(2LL,(ll)n,(ll)Mod)%Mod)%Mod;
165         an=(ll)an*powMM(3LL,(ll)n,(ll)Mod)%Mod;
166         printf("%d
",an);
167     }
168     return 0;
169 }
  • 相关阅读:
    宝物筛选
    [HAOI2008]糖果传递
    线段树（区间查询，区间修改）——标记永久化版
    图的割边
    图的割点
    P2066 机器分配
    SP1700 TRSTAGE
    P4568 [JLOI2011]飞行路线
    POJ 2533 Longest Ordered Subsequence
    HDU 2512 一卡通大冒险
  • 原文地址：https://www.cnblogs.com/quintessence/p/7326464.html
Copyright © 2011-2022 走看看