本章节主要讲的是各种数据类型如何使用二进制的格式存储在计算机内部,这里有几个概念,计算机这种使用二进制存储的格式称为位模式(bit pattern),它是0和1的组合,有时也叫位流
- 存储数字
上一章已经可以使用二进制转换十进制了,但是还要解决正负符号问题和小数点的问题。不同的表示法有不同的处理方式,对于小数点,分为定点和浮点,第一种当没有小数部分的时候,把数字当做整数处理,这是没有小数点,也不处理小数,
第二种有小数部分- 存储整数
存储整数的时候,假定一个小数点,但是不存储,如果不足
但是这样存储有一个问题,现在电脑基本都是64位的,可能很少出现溢出的问题,如果这个电脑是4位的,那么它用来存储最大的无符号整数的话就是2的四次方,如果超出这个范围就会溢出,最高一位就会丢弃,所以,有可能会使用实数的
存储方式存储整数,为了计算机内存的使用,无符号整数和有符号整数用不同的方法存储在计算机内部。-
无符号表示法
无符号整数就是没有符号的整数,这个整数的最大值受到计算机分配的位数的限制,例如64位的电脑,最大值就是2的64次方减一,存储一个无符号整数,首先将他转化为二进制数,如果不足位数,就在左边补上零,如果超出,就会
溢出。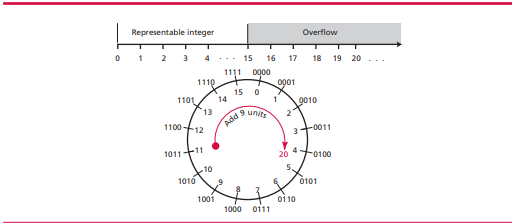
上面这个图显示了溢出之后的状况,如果你原本的数字是11,就是1011,本机是四位机子,用来存储的最高无符号整数是2次方减一就是15,当11加上9的时候,原本应该得到20,但是因为发生了溢出,第一位直接丢失,所以得到了
结果是4.
无符号整数的应用: 计数,寻址(指针),为其他数据类型排序 -
符号加绝对值表示法
这个格式把无符号整数的有效范围分成了两个相等的方法,前半个范围为正整数,后半个范围为负整数,位数的首个位表示正负,0代表正,1代表负
值得注意的是这里有两个零,分别是正0和负0.
符号加绝对值的应用:存储实数,采样模拟音频 -
二进制补码表示法
重头戏来了,二进制补码,我感觉这个表示法就是用来进行计算的,后面会看到计算的好处。
首先介绍一下反码,补码。
反码:按位取反即为反码
补码:反码加一

补码的作用之一就是模运算,为的就是把加法变减法,例如我现在设定16为模,计算15-2,其实我可以算出2的补码,模16,2的补码14,把式子变成15+14,就是29,像我们上面说的无符号整数是有最高长度的,这里的长度其实就是模,所以
29-16=13(放在二进制中就是最高位丢失),而15-2的结果也正是13.
所以无论是补码还是反码我们要解决的问题就是计算,这些都是为了实现二进制中的加减乘除。
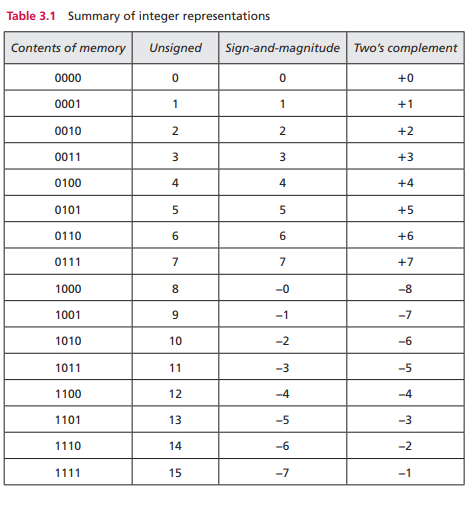
在计算机存储整数时,如果是大于或等于0的整数,直接存储,如果是负整数,那么取其补码存储。
上面那张图显示了二进制补码表示法各个数的访问,和符号绝对值表示法不同的是,这里1000后的数不是递增,而是递减的,为什么要这样做呢?很简单,我们把0001进行补码,1111也就是-1,也正是这一点其实为什么最左的符号位可以参加运算
说是符号位,但是不要把它理解成符号,还是理解成模运算, 0000到0111 只要取补码,就一定有对应的补码,比如0111取补码就是1001,所以说到底还是模运算,但我们不把第一位理解成符号时(符号时给人用的,计算机并不需要),第一位一定是1,这不是设计好的,而是计算的结果,正整数补码开头一定是1,然后把减法变加法后,如果模运算丢掉最高位后,得到的就是正确的数,用通俗的话说,负数就是减法,再把减法变加法,超出丢掉剩下就是正确的值,所以符号位其实人强加上去的,只不过运用了模运算的规则。这也是为什么没有零的原因了,因为如果有零,最高位内的数个数就不能取模了,也就是无法取反码了。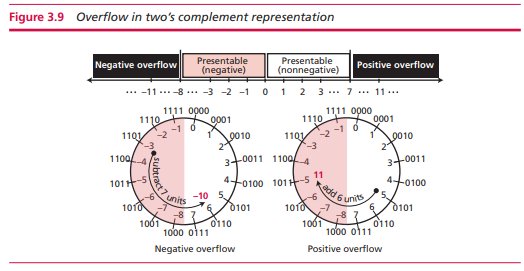
-
- 存储整数
-
小结
-
存储实数
实数是带有小数和整数部分的数,所以如果我们使用前面的定点表示法的话就会造成进度丢失,例如我们存储0.01这个数,那么小数点之后是不存储的,小数点后面的数就会丢失。用于表示实数的解决方法是浮点数。
该表示法允许小数点浮动起来,实际上就是转化为科学计数法
转换为科学计算法之后我们只存储是三个地方,符号:正负,指数:小数点移动的位数,尾数:小数点右边的二进制数
-
余码系统
为了让存储的指数都是正数,进行计算的时候不用考虑符号(这个表示方法其实和补码差不多),我们将整个位数系统偏移一定的数字,如果是四位,那就是偏移2的四次方-1
-
-
IEEE标准
电气和电子工程师协会定义了一种浮点数存储的标准,基本上是我们非常熟悉的单精度和双精度存储。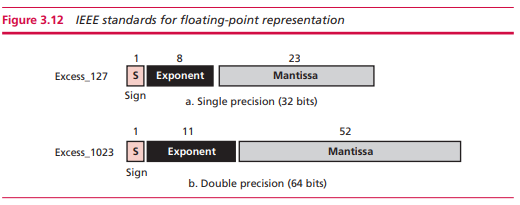
两种精度的区别在于指数的存储,上面个单精度的偏移量是2的8次方,下面那个是2的16次方。

直接上例子吧。首先判断正负,5.75是正,s=0,然后转化为二进制,101.11, 然后在进行科学计数法,尾数1.0111,指数2,2再加上偏移量127就是129啦,所以 E=10000001,M就是0111后面补足位数,小数点左边的1是不用存储的,因为在二进制中不是0就是1
但是在规定的时候,在科学计数法就规定小数点定在非零数后,所以一定是那一位一定是1.
书中原话是说implicit,就是隐含的意思。
-
存储0
为了存储0.0,符号位,指数,尾数都存上0 -
截断误差
哪怕有了双精度和单精度,依然会有尾数超过最高存储尾数的时候,如果发生这种情况,过高的位数还是会截断。称这种情况为截断误差
- 存储文本
文本说白了就是符号,表达一个语言上意义的符号,我们使用不同的位模式来表示不同的符号,所谓的位模式,就是0和1的排列组合,比如0101就表示为“我”这个符号,那么全世界这么多国家,这么多语言符号一共需要多少个位模式呢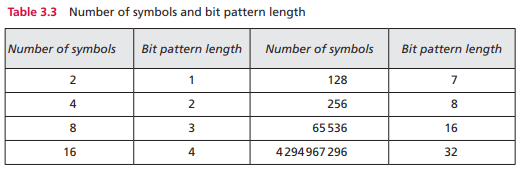
左边是符号数量,右边是位模式需要的进度,实际上是一个log函数
不同的位模式集合被设计用于表示文本符号,每一个集合称为代码,表示符号的过程被称为编码
-
存储音频
文字和数字都是有着可数的实体,但是声音没有,我们没办法"记录"声音,我们只能记录声音的密度,存储一个音频星号的密度。
哪怕是这样存储,我们也无法储存所有的值,因为那要无数的内存。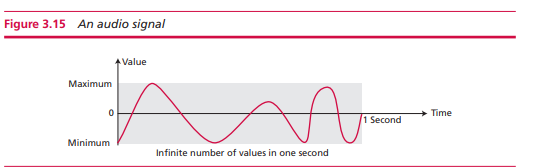
单位时间内信号随时间的变化,虽然我们不能采集所有的信号,但是我们可以记录其中的一些,这就是采样。
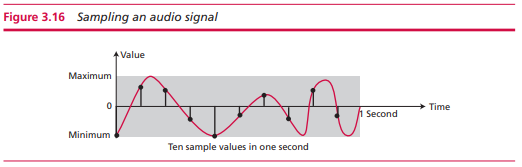
这里还涉及到采样率,也就是说我们要采集多少数据才能保证接近原本的声音呢?在内存空间和还原声音之间做一个取舍,书中给出的采样是每秒钟40000个数
量化:采样后还要进行量化,世界上就是将采样后的数据转化为无符号整数方便存储。
编码:被量化后的采样值还要进行编码,就是选择合适的位模式,比如以前是8位的,现在64的机子,那就可以编码为64位的。这个也被称为每样本位,就是每一个样本存储的位。把样本数量乘以每样本位就是位率。
编码标准:
MP3:每样本位16位,每秒44100个样本位 -
存储图像
-
光栅图
光栅图也被称为位图,就是把图像分割为一个个小方块,然后记录每个小方块的数据密度(色彩),看到这里我觉得无论哪一个多媒体形式,其实都是模拟数据,模拟声音,模拟图像,只要模拟数据的话,就会涉及到采样,只不过声音采样的是随时间变化
的值,图像采样的就是随空间变化的值。
解析度:每个方块需要记录多少的像素
色彩深度:用于表示像素位的数量,依赖于像素的颜色有不同的编码技术来处理-
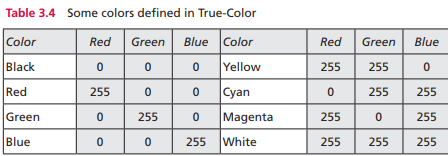
真彩色:使用24位来编码一个像素。每个RGB都表示为8位。每种原色都可以用0-255之间的数表示
-
索引色
真彩色可以表示2的24次方的颜色数量,但是如果不需要这么多的颜色那就使用索引色。从真彩色的数量中选取256中颜色,然后对其建立索引,所以只需要8位就可以保证图像是正常的,感觉索引色说白了就是采样率低了一点,比如有两个相近的颜色,那么索引色只取其中一个,老实说如果像素不高的情况下,确实可以使用这样的情况,如果像素太高,采样率越高,区别越大。
jpg使用真彩色,而gif使用索引色
-
-
矢量图
光栅图的方式有一定的缺陷,就是无法进行缩放和裁剪,无论是广大还是缩小,要么图片失真(扩大采样数量,但是有没有储存那么多的色彩)要么就是图片精度损失(缩小后一些颜色丢失),所以矢量图储存的是几何图形的,把画面中的集合图形转化为公式进行存储。
-