Sigmoid函数导数图像如下,函数最大值约为0.25

根据BP算法,每次更新的权值会是多层sigmoid prime的乘积,随着层数增多会越来越小。
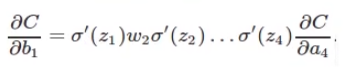
ReLu函数
f(x)=max(0,x),导数在x>0时为1,x<0时为0。

使用ReLu可以一定程度减小运算量,避免层数增加的问题。
下面代码中,仅需把sigmoid替换成relu。
1 # coding:utf8 2 import cPickle 3 import numpy as np 4 5 class Network(object): 6 def __init__(self, sizes): 7 self.num_layers = len(sizes) 8 self.sizes = sizes 9 self.biases = [np.random.randn(y, 1) for y in sizes[1:]] # L(n-1)->L(n) 10 # self.weights = [np.random.randn(y, x) 11 self.weights = [np.random.randn(y, x)/np.sqrt(x) # improved weight initializer 12 for x, y in zip(sizes[:-1], sizes[1:])] 13 14 def feedforward(self, a): 15 for b_, w_ in zip(self.biases[:-1], self.weights[:-1]): 16 # a = self.sigmoid(np.dot(w_, a)+b_) 17 a = self.relu(np.dot(w_, a)+b_) 18 # a=self.sigmoid(np.dot(self.weights[-1], a)+self.biases[-1]) 19 a=self.relu(np.dot(self.weights[-1], a)+self.biases[-1]) 20 # a=self.softmax(np.dot(self.weights[-1], a)+self.biases[-1]) # add for softmax 21 return a 22 23 def SGD(self, training_data, test_data,epochs, mini_batch_size, eta=1.0, lambda_=0.1): 24 n_test = len(test_data) 25 n = len(training_data) 26 cx=range(epochs) 27 for j in cx: 28 self.cost = 0.0 29 np.random.shuffle(training_data) # shuffle 30 for k in xrange(0, n, mini_batch_size): 31 mini_batch = training_data[k:k+mini_batch_size] 32 self.update_mini_batch(mini_batch, eta,n) 33 self.cost+=0.5*lambda_*sum(np.linalg.norm(w_)**2 for w_ in self.weights) 34 print "Epoch {0}: cost={1} {2} / {3}, {4} / {5}".format(j, self.cost/n, 35 self.evaluate(training_data,1), n,self.evaluate(test_data), n_test) 36 37 def update_mini_batch(self, mini_batch, eta, n, lambda_=0.1): 38 for x, y in mini_batch: 39 delta_b, delta_w = self.backprop(x, y) 40 for i in range(len(self.weights)): # L2 regularization 41 self.weights[i]-=eta/len(mini_batch)*(delta_w[i] +lambda_/n*self.weights[i]) 42 self.biases -= eta/len(mini_batch)*delta_b 43 a=self.feedforward(x) 44 # cost=np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a))) cost entropy 45 cost=0.5*np.sum((a-y)**2) 46 self.cost += cost 47 48 def backprop(self, x, y): 49 b=np.zeros_like(self.biases) 50 w=np.zeros_like(self.weights) 51 a_ = x 52 a = [x] 53 for b_, w_ in zip(self.biases, self.weights): 54 # a_ = self.sigmoid(np.dot(w_, a_)+b_) 55 a_ = self.relu(np.dot(w_, a_)+b_) 56 a.append(a_) 57 for l in xrange(1, self.num_layers): 58 if l==1: 59 # delta= self.sigmoid_prime(a[-1])*(a[-1]-y) # O(k)=a[-1], t(k)=y 60 delta= a[-1]-y # cross-entropy 61 # delta=self.softmax(np.dot(w_, a[-2])+b_) -y # add for softmax 62 else: 63 #sp = self.sigmoid_prime(a[-l]) # O(j)=a[-l] 64 sp=self.relu_prime(a[-l]) 65 delta = np.dot(self.weights[-l+1].T, delta) * sp 66 b[-l] = delta 67 w[-l] = np.dot(delta, a[-l-1].T) 68 return (b, w) 69 70 def evaluate(self, test_data, train=0): 71 test_results = [(np.argmax(self.feedforward(x)), y) 72 for (x, y) in test_data] 73 if train: 74 return sum(int(x == np.argmax(y)) for (x, y) in test_results) 75 else: 76 return sum(int(x == y) for (x, y) in test_results) 77 78 def sigmoid(self,z): 79 return 1.0/(1.0+np.exp(-z)) 80 81 def sigmoid_prime(self,z): 82 return z*(1-z) 83 84 def softmax(self,a): 85 m = np.exp(a) 86 return m / np.sum(m) 87 88 def relu(self,z): 89 return np.maximum(z, 0.0) 90 91 def relu_prime(self,z): 92 z[z>0]=1 # <numpy.core._internal._ctypes> 93 return z 94 95 def get_label(i): 96 c=np.zeros((10,1)) 97 c[i]=1 98 return c 99 100 if __name__ == '__main__': 101 def get_data(data): 102 return [np.reshape(x, (784,1)) for x in data[0]] 103 104 f = open('mnist.pkl', 'rb') 105 training_data, validation_data, test_data = cPickle.load(f) 106 training_inputs = get_data(training_data) 107 training_label=[get_label(y_) for y_ in training_data[1]] 108 data = zip(training_inputs,training_label) 109 test_inputs = training_inputs = get_data(test_data) 110 test = zip(test_inputs,test_data[1]) 111 net = Network([784, 30, 10]) 112 net.SGD(data[:5000],test[:5000],epochs=30,mini_batch_size=10, eta=0.1, lambda_=1.0)