题目描述
参与考古挖掘的小明得到了一份藏宝图,藏宝图上标出了 nn 个深埋在地下的宝藏屋, 也给出了这 nn 个宝藏屋之间可供开发的mm 条道路和它们的长度。
小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是,每个宝藏屋距离地面都很远, 也就是说,从地面打通一条到某个宝藏屋的道路是很困难的,而开发宝藏屋之间的道路 则相对容易很多。
小明的决心感动了考古挖掘的赞助商,赞助商决定免费赞助他打通一条从地面到某 个宝藏屋的通道,通往哪个宝藏屋则由小明来决定。
在此基础上,小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以 任意通行不消耗代价。每开凿出一条新道路,小明就会与考古队一起挖掘出由该条道路 所能到达的宝藏屋的宝藏。另外,小明不想开发无用道路,即两个已经被挖掘过的宝藏 屋之间的道路无需再开发。
新开发一条道路的代价是:
mathrm{L} imes mathrm{K}L×K
L代表这条道路的长度,K代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的 宝藏屋的数量(包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋) 。
请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路,使得工程总代 价最小,并输出这个最小值。
输入输出格式
输入格式:
第一行两个用空格分离的正整数 n,mn,m,代表宝藏屋的个数和道路数。
接下来 mm 行,每行三个用空格分离的正整数,分别是由一条道路连接的两个宝藏 屋的编号(编号为 1-n1−n),和这条道路的长度 vv。
输出格式:
一个正整数,表示最小的总代价。
输入输出样例
说明
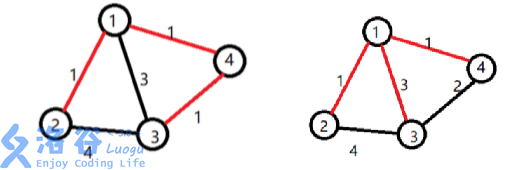
【样例解释1】
小明选定让赞助商打通了11 号宝藏屋。小明开发了道路 1 o 21→2,挖掘了 22 号宝 藏。开发了道路 1 o 41→4,挖掘了 44号宝藏。还开发了道路 4 o 34→3,挖掘了33号宝 藏。工程总代价为:1 imes 1 + 1 imes 1 + 1 imes 2 = 41×1+1×1+1×2=4
【样例解释2】
小明选定让赞助商打通了11 号宝藏屋。小明开发了道路 1 o 21→2,挖掘了 22 号宝 藏。开发了道路 1 o 31→3,挖掘了 33号宝藏。还开发了道路 1 o 41→4,挖掘了44号宝 藏。工程总代价为:1 imes 1 + 3 imes 1 + 1 imes 1 = 51×1+3×1+1×1=5
【数据规模与约定】
对于20\%20%的数据: 保证输入是一棵树,1 le n le 81≤n≤8,v le 5000v≤5000 且所有的 vv都相等。
对于 40\%40%的数据: 1 le n le 81≤n≤8,0 le m le 10000≤m≤1000,v le 5000v≤5000 且所有的vv都相等。
对于70\%70%的数据: 1 le n le 81≤n≤8,0 le m le 10000≤m≤1000,v le 5000v≤5000
对于100\%100%的数据: 1 le n le 121≤n≤12,0 le m le 10000≤m≤1000,v le 500000v≤500000
题解
NOIP2018rp++!!!
去年考场上用了刚学两个星期的最小生成树,还不是像大佬们一样的prim我用的Kruscal(prim不会啊qwq),还觉得自己贼哩玛流脾怕是要第一场noip就400+了qwq
最小生成树最后当然是喜提45qwq
现在回过头来看,发现,
这么小的数据当然是要爆搜啊!qwq
首先,$n$这么小,不妨枚举起点。
枚举起点之后怎么搜?!怎么搜?!(不知所措
用一个int记录状态,第$j$位为$1$为存在,为$0$为不存在。
实际实现中不写作$1<<(j-1)$而写作$1<<j$,因为好写又快一点。
然后在dfs里面用两个for循环,一个for在树上的点,一个for不在树上的点,如果有边就dfs。
中间记得最优性剪枝就好啦qwq
1 /* 2 qwerta 3 P3959 宝藏 Accepted 4 100 5 代码 C++,0.87KB 6 提交时间 2018-10-30 20:08:08 7 耗时/内存 241ms, 940KB 8 */ 9 #include<iostream> 10 #include<cstring> 11 #include<cstdio> 12 #include<cmath> 13 using namespace std; 14 int g[13][13];//边 15 int ans; 16 int d[13];//深度 17 int n; 18 const int INF=500003; 19 int f[8003];//状态为k时的最小费用记为f[k] 20 int to; 21 void dfs(int fe,int k) 22 { 23 if(k==to)//如果每个点都有了 24 { 25 ans=min(ans,fe); 26 return; 27 } 28 if(fe>=ans)return;//超过答案return 29 if(fe>=f[k])return;//不如之前扫这个点的结果return 30 f[k]=fe;//更新该状态最小费用 31 for(int i=1;i<=n;++i) 32 if((k|(1<<i))==k)//如果i点在树上 33 { 34 for(int j=1;j<=n;++j) 35 { 36 if(((k|(1<<j))!=k)&&g[i][j]<INF)//如果j点不在树上并且i,j间有边 37 { 38 d[j]=d[i]+1;//更新j的深度 39 dfs(fe+g[i][j]*d[j],(k|(1<<j)));//往下搜 40 } 41 } 42 } 43 return; 44 } 45 int main() 46 { 47 //freopen("a.in","r",stdin); 48 int m; 49 scanf("%d%d",&n,&m); 50 memset(g,127,sizeof(g)); 51 for(int i=1;i<=m;++i) 52 { 53 int u,v,l; 54 scanf("%d%d%d",&u,&v,&l); 55 g[u][v]=min(g[u][v],l);//重边取最小值就好了 56 g[v][u]=g[u][v]; 57 } 58 ans=n*n*500000+3;//ans=INF 59 to=0; 60 for(int i=1;i<=n;++i) 61 to+=(1<<i);//to为目标态(所有点都有 62 for(int i=1;i<=n;++i) 63 { 64 memset(f,127,sizeof(f));//重置f(在不同的根下的f不兼容 65 int s=i; 66 d[s]=0; 67 dfs(0,(1<<s)); 68 } 69 cout<<ans<<endl;//输出 70 return 0;//撒花 71 }