题目描述
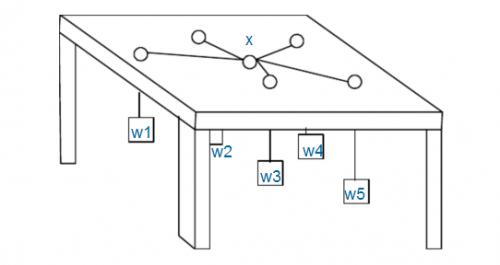
如图:有n个重物,每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞,然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的(不会造成能量损失),桌子足够高(因而重物不会垂到地上),且忽略所有的摩擦。
问绳结X最终平衡于何处。
注意:桌面上的洞都比绳结X小得多,所以即使某个重物特别重,绳结X也不可能穿过桌面上的洞掉下来,最多是卡在某个洞口处。
输入输出格式
输入格式:
文件的第一行为一个正整数n(1≤n≤1000),表示重物和洞的数目。接下来的n行,每行是3个整数:Xi.Yi.Wi,分别表示第i个洞的坐标以及第 i个重物的重量。(-10000≤x,y≤10000, 0<w≤1000 )
输出格式:
你的程序必须输出两个浮点数(保留小数点后三位),分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。
输入输出样例
说明
[JSOI]
题解
这道题一开始看到觉得要向量什么的......计算几何?!qwq
对同学讲的在$sum_{i=1}^{n}l_i*w_i$取最小值时最优也不是很能理解......
然后题解中有一种说法↓

觉得还是能强行理解的。(大概模拟退火都需要神仙思路吧qwq
然后就套模拟退火的板子就行了。
调(试)参(探)过程中感受了一下srand(19*****7)的魅力,和clock()/CLOCKS_PER_SEC的神仙用途。
//就是听说clock()很慢qwq,不知道用来优化爆搜效果好不好
然后就是代码了qwq↓
1 /* 2 qwerta 3 P1337 [JSOI2004]平衡点 / 吊打XXX Accepted 4 100 5 代码 C++,1.05KB 6 提交时间 2018-11-01 18:28:16 7 耗时/内存 7005ms, 816KB 8 */ 9 #include<iostream> 10 #include<cstdlib> 11 #include<cstdio> 12 #include<ctime> 13 #include<cmath> 14 using namespace std; 15 struct emm{ 16 int x,y,w; 17 }a[1003]; 18 int n; 19 double check(double x,double y)//返回(x,y)的那个sum值 20 { 21 double now=0; 22 for(int i=1;i<=n;++i) 23 { 24 double mx=a[i].x-x,my=a[i].y-y; 25 now+=sqrt(mx*mx+my*my)*a[i].w; 26 } 27 return now; 28 } 29 double ansx,ansy,ans; 30 double t,tmin=1e-14; 31 double deltt=0.993; 32 void SA()//板子 33 { 34 double x=ansx,y=ansy; 35 t=6000;//2333不给过,被改成6000就过掉了qwq 36 while(t>tmin) 37 { 38 double tox=x+((rand()<<1)-RAND_MAX)*t; 39 double toy=y+((rand()<<1)-RAND_MAX)*t; 40 double now=check(tox,toy); 41 double delt=now-ans; 42 if(delt<0) 43 { 44 ans=now,ansx=tox,ansy=toy; 45 x=tox,y=toy; 46 } 47 else if(exp(-delt/t)*RAND_MAX>rand()){x=tox,y=toy;} 48 t*=deltt; 49 } 50 return; 51 } 52 int main() 53 { 54 //freopen("a.in","r",stdin); 55 srand(19260817);srand(rand()),srand(rand()); 56 scanf("%d",&n); 57 int totx,toty; 58 for(int i=1;i<=n;++i) 59 { 60 scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].w); 61 totx+=a[i].x,toty=a[i].y; 62 } 63 ans=1e14+2333,ansx=totx/n,ansy=toty/n;//从中间开始跑 64 while((double)clock()/CLOCKS_PER_SEC<0.75)//如果用掉的时间还不超过0.75秒 65 SA(); 66 printf("%.3f %.3f",ansx,ansy); 67 return 0; 68 }
吸毒真香