2019.9.1 涂抹果酱

 

---

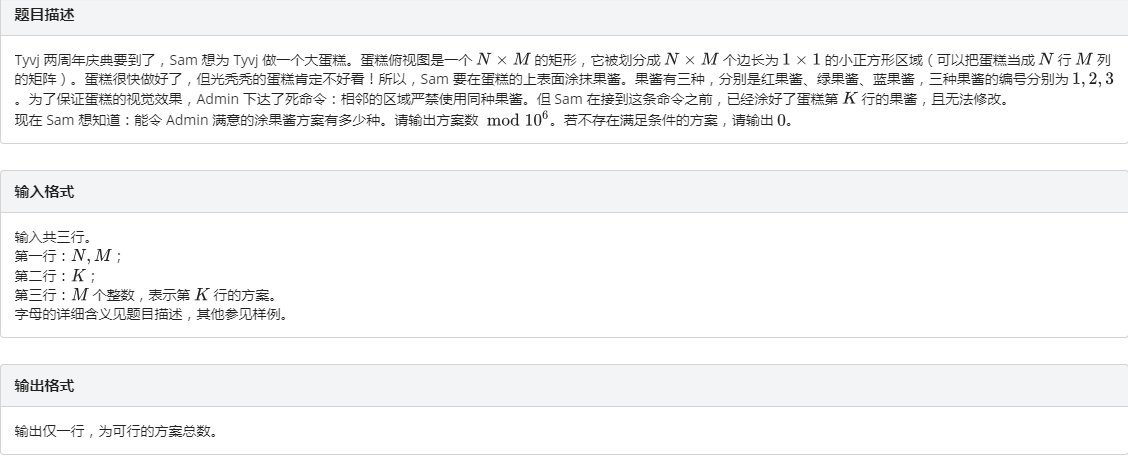
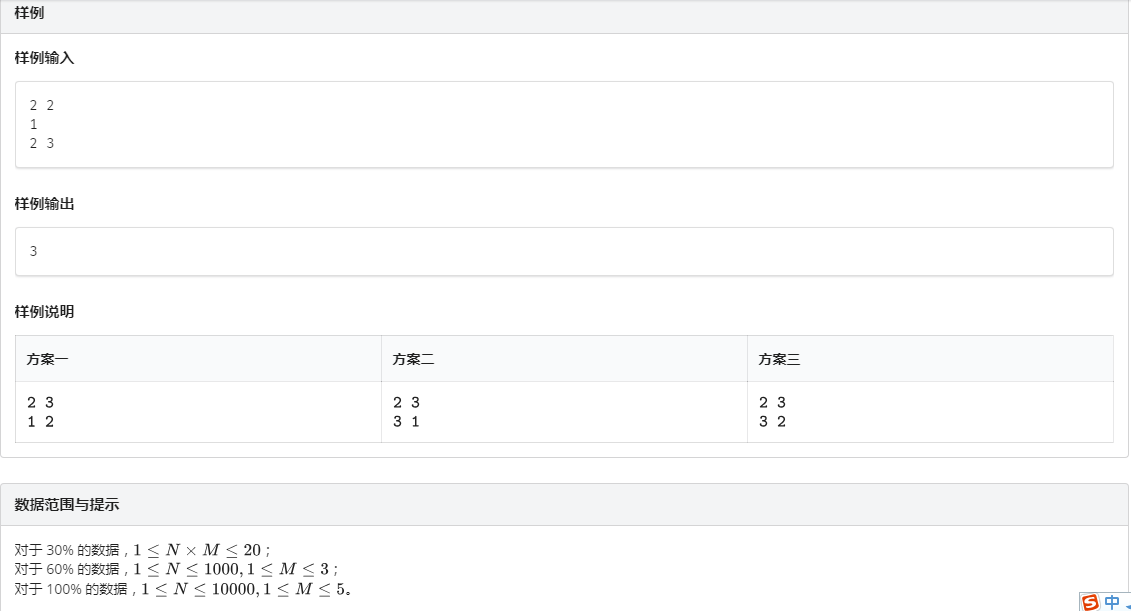
还是简单的状压dp

用dp[i][j]表示前i行最后一行状态是j的方案总数

则每次判断当前是普通行、已经固定的行、固定行的下一行

如果是普通行 dp[i][j]+=dp[i-1][l]

如果是固定行 记已经固定好的状态编号是flag 则dp[i][flag]+=dp[i-1][l]且dp[i][j](j!=flag)=0

如果是固定行的下一行 则dp[i][j]+=dp[i-1][flag]

注意由于是1-3所以用4进制状态压缩 所有含有0的状态全部排除

上代码

#include<iostream>
#include<cstdio>
#include<cstring>
#define int long long
using namespace std;
int cnt,num[10050],dp[10050][(2<<12)+1];
int n,m,k,mapp[10050],ans,book;
bool check(int x)
{
    int flag=-1;
    if(x==0)return false;
    int idx=0;
    int temp=x;
    while(temp)
    {
        if(!(temp%4))return false;
        idx++;
        temp/=4;
    }
    if(idx<m)return false;
    while(x)
    {
        if(flag==x%4)return false;
        flag=x%4;
        x/=4;
    }
    return true;
}//判断状态本身是否合法
bool cannot(int x,int y)
{
    while(x)
    {
        int p=x%4,q=y%4;
        if(p==q)return true;
        x/=4,y/=4;
    }
    return false;
}//判断两个状态能否作为上下两行同时出现
signed main()
{
    scanf("%lld%lld",&n,&m);
    scanf("%lld",&k);
    for(int i=1;i<=m;i++)scanf("%lld",&mapp[i]),book=book*4+mapp[i];
    if(!check(book))//特判，如果固定行的状态不合法
    {
        putchar('0');
        return 0;
    }
    int maxn=1;
    for(int i=1;i<=m;i++)maxn*=4;
    --maxn;
    for(int i=0;i<=maxn;i++)
        if(check(i))//枚举可能的状态
        {
            //printf("%d
",i);
            num[++cnt]=i,dp[1][cnt]=1;
        }
    int flag=-1;
    for(int j=1;j<=cnt;j++)
        if(num[j]==book)
        {
            flag=j;
            break;
        }//记录固定行状态编号
    for(int i=1;i<=cnt;i++)
        if(i!=flag)dp[k][i]=0;//将所有固定行没有选择固定行状态的dp值全部置0
    for(int i=2;i<=n;i++)
    {
        if(i==k)//固定行
        {
            for(int j=1;j<=cnt;j++)
                if(j!=flag)dp[i][j]=0;
            for(int l=1;l<=cnt;l++)
                if(!cannot(num[l],book))dp[i][flag]=(dp[i][flag]+dp[i-1][l])%1000000;//枚举上一行的状态，记得加的时候取模
            continue;
        }
        for(int j=1;j<=cnt;j++)
        {
            int x=num[j];
            if(i==k+1)//固定行的上一行
            {
                if(cannot(x,book))continue;
                dp[i][j]=(dp[i][j]+dp[i-1][flag])%1000000;
                continue;
            }
            for(int l=1;l<=cnt;l++)
            {
                int y=num[l];
                if(cannot(x,y))continue;
                dp[i][j]=(dp[i][j]+dp[i-1][l])%1000000;
            }//普通行
        }
    }
    for(int i=1;i<=cnt;i++)
    {
        ans=(ans+dp[n][i])%1000000;//枚举最后一行可能的状态
        //printf("%lld ",ans);
    }
    printf("%lld",ans);
    return 0;
}