一、并查集基础
(一)引入
我们先来看一个问题。
某学校有N个学生,形成M个俱乐部。每个俱乐部里的学生有着一定相似的兴趣爱好,形成一个朋友圈。一个学生可以同时属于若干个不同的俱乐部。根据“我的朋友的朋友也是我的朋友”这个推论可以得出,如果A和B是朋友,且B和C是朋友,则A和C也是朋友。请编写程序计算最大朋友圈中有多少人。
输入格式:
输入的第一行包含两个正整数N(≤30000)和M(≤1000),分别代表学校的学生总数和俱乐部的个数。后面的M行每行按以下格式给出1个俱乐部的信息,其中学生从1~N编号:
第i个俱乐部的人数Mi(空格)学生1(空格)学生2 … 学生Mi
输出格式:
输出给出一个整数,表示在最大朋友圈中有多少人。
输入样例:
7 4
3 1 2 3
2 1 4
3 5 6 7
1 6
输出样例:
4
我们把这个题抽象化:
现在有n个数,它们按照一定规律合并,形成一些集合,求最大集合的元素个数。
这个合并规律如下:
(1)同一个俱乐部的所有人属于同一个集合;
(2)若两个俱乐部包含同一个人,则这两个俱乐部属于同一个集合。
按照正常做法,我们对于每一个人按照上述规律扫描剩余的人,运行复杂度O(n^很大)。
这个方法显然过不了。
我们重新分析这个题目,主要难点有两个:
第一,对于第一条,同一个俱乐部的所有人如何存储它们所在同一个集合内。
这个很好解决,我们再开一个book数组,对于每一个人i,假设它在cnt集合内,我们标记book[i]=cnt。
如果这样标记,对于第二个合并规律,我们扫描另一个俱乐部的所有人,我们把每一个book[i]都置成要合并到的俱乐部,总复杂度O(nm)。
但这样还是过不了,所以我们考虑把第二个合并步骤的复杂度优化到O(1),也就是说我们只需要修改一个数就可以修改整个集合。
对于这样的修改方式,我们可以想到一种数据结构——树。
利用树存储每个集合有两个好处:
第一,每棵树只有一个树根(也就是查找树根就可以查找整棵树)
第二,两棵树合并只需要把一棵树的树根接到另一棵上(所以修改的复杂度是O(1))。
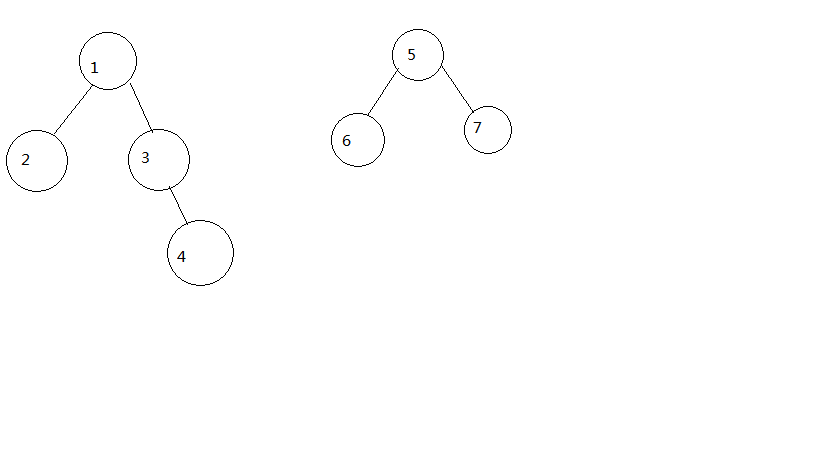
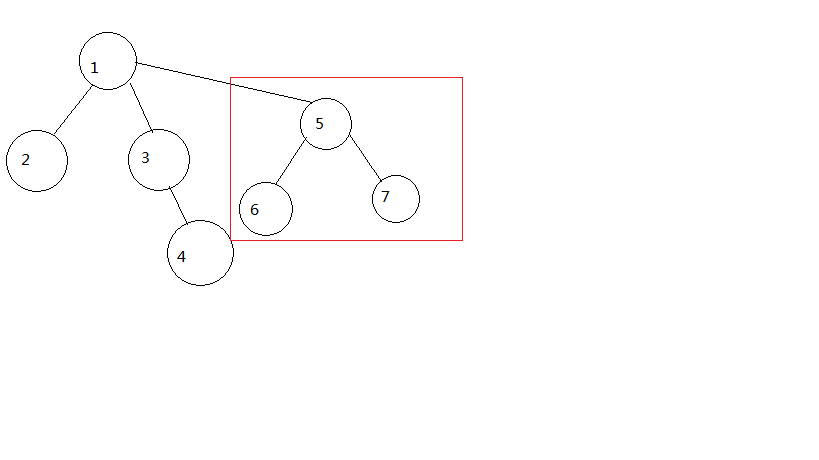
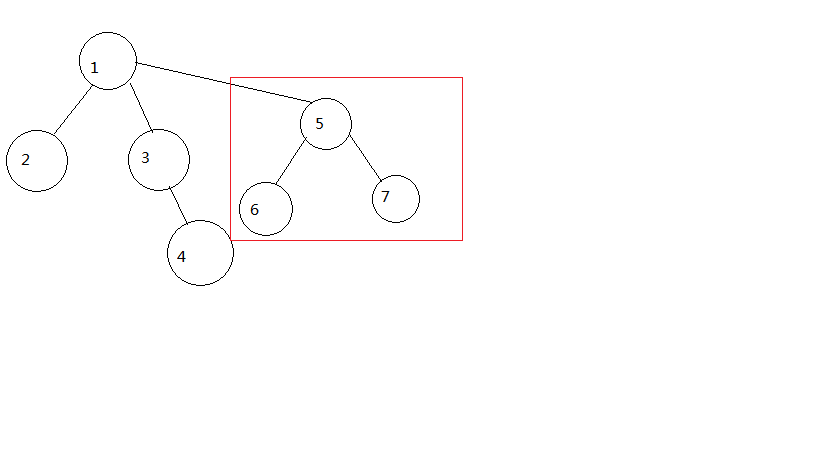
大概就是上面这么合并
也就是说我们可以用树优化查找和合并集合的过程,其本质就是对树之间的处理。
又因为,这一类题的根本步骤就是查找与合并,所以我们把这样的数据结构叫做并查集。
(二)并查集的基本操作
刚才我们已经知道,并查集中合并两个元素实际上是合并他们所在树的祖先。
为了查询这两个点是否在一棵树上,我们首先要找到他们两个点的祖先分别是谁,并判断他们的祖先是否是同一个点即可。
但是因为树会退化成一条链,所以我们在查找祖先时要把下图的第一个树变成第二个树,这是后话。


第二个图的意思就是所有的点都连到根节点上。
我们暂且不提怎么查找一个点的祖先,在我们查找两个点祖先之后,判断他们的祖先是不是同一个点,如果不是同一个点合并即可。
所以我们用fa[x]表示x的父亲,则代码如下:
void u(int a,int b)
{
int c=f(a),d=f(b);
if(fa[c]!=fa[d])
{
fa[min(c,d)]=fa[max(c,d)];
return;
}
}
一定要注意的是,绝对不能让fa[min(a,b]直接等于fa[max(a,b)],因为这样只合并了两个点,而不是其所在的树。
同时,注意合并时要按照一定的大小顺序,所以这里是按小往大合的。
所以这是合并两个点的方法。
关于查找祖先的方法,有一个非常绝妙的方法:
int f(int o)
{
if(fa[o]==o)return o;
return fa[o]=f(fa[o]);
}
第一行非常容易理解,如果o的祖先时自己则它自己就是这棵树的祖先。
第二行我们把它分解成两部分:
(1)f(fa[o])找到fa[o]的祖先。
(2)return fa[o]=f(fa[o]) 将o的父亲置为其父亲的祖先
也就是说 我们成功把一棵近似于一条链的树 弄成了一棵最多只有三层的树。
这个过程换句话说是这样:
(1)递归地找点o每一级祖先o',直到找到它真正的祖先o1;
(2)回溯,对于每一个o',将fa[o]置为o1.
也就是说 通过这个步骤,这棵树的每一个点都直接连接到了祖先上
所以回到这章开始的部分,对于那两棵树之间的变化,有一种方法就是上面说的更改每个点与祖先的连接方式,这种方式叫作路径压缩。
其实还有一个稍微好实现一点的方法,对于每个树根,我们记录它所在的树的高度,把这个高度叫作这棵树的秩。
对于每个合并操作(不是路径压缩时的查找操作),我们把秩小的树合到秩大的树上,这样可以保证合出来的新树的秩不大于原来任何一棵树。
若两棵树的秩一样,则新树的秩是原树的秩+1.
这种方法也叫按秩合并。
最后记得一开始初始化,令fa[x]=x。
上个板子:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int fa[100050];
int f(int o)
{
if(fa[o]==o)return o;
return fa[o]=f(fa[o]);
}
void u(int a,int b)
{
int c=f(a),d=f(b);
if(c!=d)fa[min(c,d)]=fa[max(c,d)];
return;
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=m;i++)
{
int x,y,opt;
scanf("%d%d%d",&x,&y,&opt);
if(!opt)u(x,y);
else
{
if(f(x)!=f(y))puts("NO");
else puts("YES");
}
}
return 0;
}
高级用法待填坑。