一个月以前学的最近公共祖先。一直以为我理解的最够深刻了,直到遇见真的比较复杂的题之后,才发现自己的漏洞。
那么今天就借助一道模板题来总结一下吧。
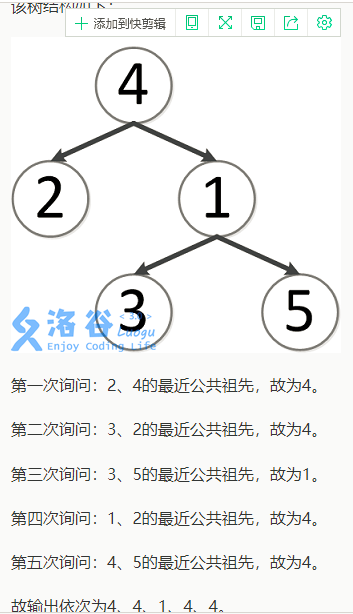
下面是洛谷模板的题面。


下面是样例及解释。
Input
5 5 4 3 1 2 4 5 1 1 4 2 4 3 2 3 5 1 2 4 5
Output
4 4 1 4 4
那么接下来就详细说说LCA是怎么回事吧。
首先是一般的LCA。
 (我是盗图小丸子,对图作者表示歉意与感谢)
(我是盗图小丸子,对图作者表示歉意与感谢)
那么我们就先举个栗子。
比如4和16的LCA就是3.而对于9和10的LCA则是7.对于17和18则又是3。
那么暴力做法就很显然了不是吗?
暴力做法
我们就以17和18为例。既然是要找LCA,那么我们就让他们往上去走。
17−>14−>10−>7−>3
18->16->12->8->5->318−>16−>12−>8−>5−>3
第一次遇到的地方就是LCA(17,18)的值了。DFS暴力实现啊?
如果你觉得会这些就足够了的话(那您可就是神了啊),TLE欢迎你。大多数题一般是不会很快(-->TLE)的。
不信我们就举个栗子吧(还是上图),比如4和18.显然这样暴力是不太好的。我们显然是希望4可以等18上去了之后再走。
那么就有一种很优秀(玄学)的LCA了。
倍增LCA
当你看到这里,这题才刚刚开始啊。
那么首先先说倍增吧(有专门讲倍增的文章这里就简单说一下啦)。
!!倍增
倍增就是按照2的n次幂来往上走。但是我们一般是从大往小跳,当用大的跳过了之后,就用小的再跳回来(好蠢的样子)。
还是举个栗子吧(还是17和18)
17−>3
18−>5−>3
这样明显就是快了不少啊。复杂度是O(nlogn);对于大多数题来说就足够了。
回到LCA
所以对于倍增LCA来说,我们就需要记录一下每一个节点的幂次方爸爸是谁了啊。
那么我们跑一遍dfs就解决了。(deep是节点的深度,fa是存某数的幂次方爸爸的)
void dfs(int f,int fath) {
deep[f]=deep[fath]+1;
fa[f][0]=fath;
for(int i=1;(1<<i)<=deep[f];i++)
fa[f][i]=fa[fa[f][i-1]][i-1];//意思是f的2^i祖先等于f的2^(i-1)祖先的2^(i-1)祖先 2^i=2^(i-1)+2^(i-1)
for(int i=head[f];i;i=edge[i].nex)
if(edge[i].t!=fath)
dfs(edge[i].t,f);
return;
}
然后我们就可以上LCA了。
在此之前,我喜欢先加一个常数的优化。(当然你也可以不加,直接套用log2(x)->x是次方,就应该也可以啊)
for(int i=1;i<=n;i++)
lg[i]=lg[i-1]+(1<<lg[i-1]==i);//看不懂就自己手推好啦,这可救不了你
然后就是LCA啦,我们想把他们都调到一个高度再找,这样就可以实现了。
int LCA(int x,int y) {
if(deep[x]<deep[y])
swap(x,y);
while(deep[x]>deep[y])
x=fa[x][lg[deep[x]-deep[y]]-1];
if(x==y)
return x;
for(int k=lg[deep[x]]-1;k>=0;k--)
if(fa[x][k]!=fa[y][k]) {
x=fa[x][k];
y=fa[y][k];
}
return fa[x][0];
}
很好,我自以为讲的还不错,勉强看吧(毕竟语文不好)。下面放完整版。
Code(代码风格2.1版)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
const int MA=5e5+1;
struct ss{
int t,nex;
}edge[2*MA];
int n,m,s,tot;
int fa[MA][22];
int lg[MA],head[MA],deep[MA];
int read() {
int x=0;
bool flag=0;
char ch=getchar();
if(ch=='-')
flag=1;
while(ch<'0'||ch>'9')
ch=getchar();
while(ch>='0'&&ch<='9') {
x*=10;
x+=ch-'0';
ch=getchar();
}
if(flag) return -x;
return x;
}//快读压行什么的,我才不要 傲娇】
void add(int x,int y) {
edge[++tot].t=y;
edge[tot].nex=head[x];
head[x]=tot;
}
void dfs(int f,int fath) {
deep[f]=deep[fath]+1;
fa[f][0]=fath;
for(int i=1;(1<<i)<=deep[f];i++)
fa[f][i]=fa[fa[f][i-1]][i-1];
for(int i=head[f];i;i=edge[i].nex)
if(edge[i].t!=fath)
dfs(edge[i].t,f);
return;
}
int LCA(int x,int y) {
if(deep[x]<deep[y])
swap(x,y);
while(deep[x]>deep[y])
x=fa[x][lg[deep[x]-deep[y]]-1];
if(x==y)
return x;
for(int k=lg[deep[x]]-1;k>=0;k--)
if(fa[x][k]!=fa[y][k]) {
x=fa[x][k];
y=fa[y][k];
}
return fa[x][0];
}
int main()
{
n=read();
m=read();
s=read();
for(int i=1;i<n;i++) {
int x=read();
int y=read();
add(x,y);
add(y,x);
}
for(int i=1;i<=n;i++)
lg[i]=lg[i-1]+(1<<lg[i-1]==i);
dfs(s,0);
for(int i=1;i<=m;i++) {
int a=read();
int b=read();
int ans=LCA(a,b);
printf("%d
",ans);
}
return 0;
}
然后我这题还能用 树链剖分,还有约束RMQ求LCA,以及tarjan求LCA(这些我全都不会)。之后会了的话会回来不上的,有兴趣的可以之后在自学一下啦。
那么就这样啦。谢谢