这题看起来长得就很像某些dfs例题,但是n=1000也太大了.
考虑怎么来搞这道题呢?注意到A处理完后B才开始处理,是否最优解一定是让A快速处理完一个物品后让B开始处理?
我们把物品分为两类:A>B的和B>A的.一定是先处理A<B的再开始处理A>B的.这样可以让A对于B>A的物品更多的缓冲时间.具体过程可以画个图.
要想快速开始处理A需要先处理A小的.要想快速结束需要最后处理B小的.按照这样的策略sort一下后输出即可.
如果还是不懂的的话可以先考虑如何输出时间吧:假装已经有了最优排列顺序你会怎样输出答案?对于A运行的时间可以一股脑全处理完是吧,suma++++.但是对于每个物品处理后的sumb不一定总是从上一个sumb直接加上来,很有可能出现b比a快的情况,这个时候需要让sumb=suma后再+=b[i].
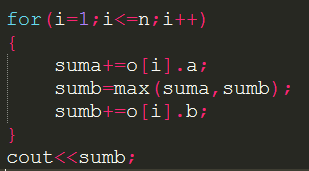
那么最后出现b比a快的时候我们需要让越靠后处理的物品b越小才能保证快速的处理完,因此sort的总策略是(没错就是一边sort后处理答案并输出) : 如果不同类的一定让A<B的排在前面.如果A都<B让A小的排前面,如果A都>B让B小的排后面.

using namespace std; struct node { int a,b; int minn,flag; }o[1010]; int i; int n,suma,sumb; inline bool Orz(node x,node y){ return x.flag==y.flag?(x.flag==0?x.minn<y.minn:x.minn>y.minn):x.flag<y.flag; } int main(){ n=read(); for(i=1;i<=n;i++) o[i].a=read(); for(i=1;i<=n;i++){ o[i].b=read(); o[i].minn=min(o[i].a,o[i].b); o[i].flag=o[i].a>o[i].b; } sort(o+1,o+1+n,Orz); for(i=1;i<=n;i++){ suma+=o[i].a; sumb=max(suma,sumb); sumb+=o[i].b; } cout<<sumb; return 0; }
这道题的难点在于能不能舍弃dfs来想贪心 和 能不能贪心后想到办法算时间(我想了一早读23333).
