p1228

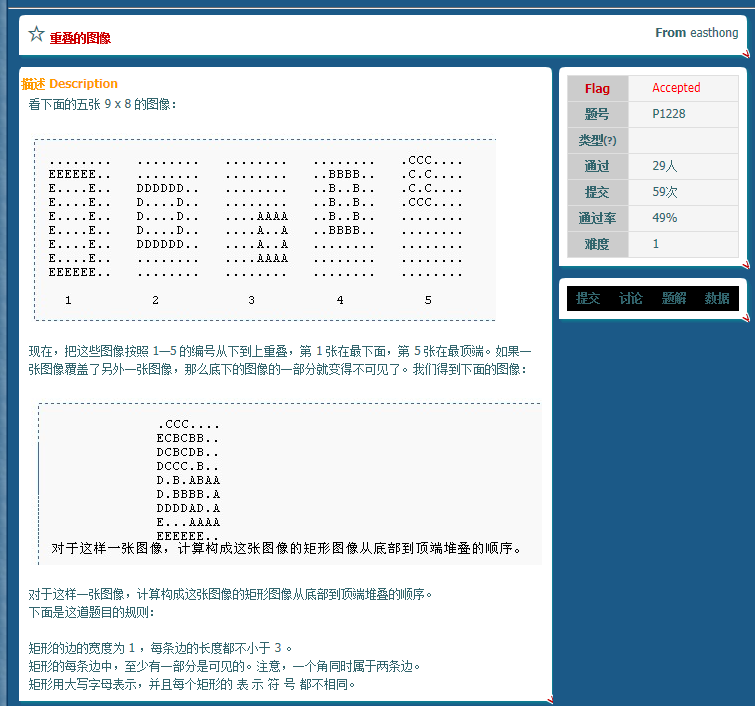
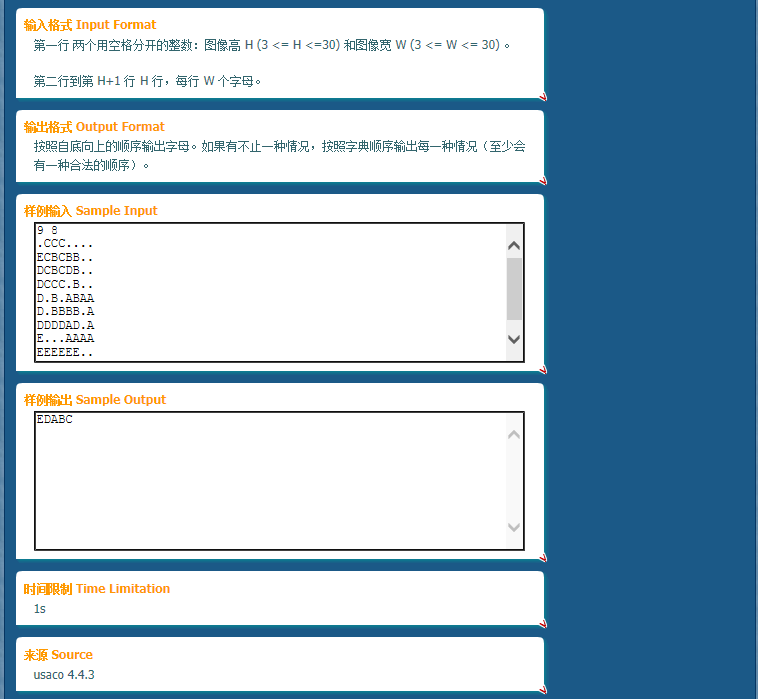
这是一道图论呦.

这怎么和图论相关呢?差分约束不是也看起来和图论无关么2333.

那么本题就类似于差分约束.考虑到矩形的每一条边都有一部分露出来,那么可以m*n的用至少四个点更新每个字母的四个顶角位置.然后对于每个有顶角的字母跑它的四个边,如果有别的字母就说明这个字母再本字母之上,连一条有向边.(在这里连的话很大几率使两点间有多个边.考虑到点最多有26个,可以写一个邻接矩阵)

这样就有了一个有向无环图,我们要做的就是按照字典序输出所有可行顺序.这个怎么弄呢?如果只输出一个的话我会维护堆后拓扑排序全部输出的话...依旧欺负它点少,我们直接上一个带dfs的回溯拓扑就好.

我写的还是个邻接表...并且记录入度和是否有点flag.对于从'a'到'z'如果flag==1且入度为0就记录答案,flag改为1,然后dfs冲进去,对于从a到z再判断一下,记录答案,所连边sum--,然后再冲进去.如果dfs层数为n时输出return,并打扫现场.

为什么这样子能做到字典序从小到大呢?因为每次把字母放进ans时是从A到Z的.而邻接表的遍历对然是逆字典序的,但是不影响答案啊.

46 .
65 A
90 Z

虽然字符和数字间可以这样转化,但是实际上并不需要这么严格,字符实际上就是数字.

using namespace std;
int i,f,t;
char ch;
char ans[100];
int n,m;
int l[100],r[100],u[100],d[100],sum[100],flag[100],a[100][100],o[100][100];
struct node{
    int x,y,next;
}e[10000];
int tot,head[100];
void add(int x,int y){
    tot++;
    e[tot].x=x;
    e[tot].y=y;
    e[tot].next=head[x];
    head[x]=tot;
}
void dfs(int now)
{
    if(now==n){
        for(int j=1;j<=n;j++)
            cout<<ans[j];
        cout<<endl;
        return;
    }
    now++;
    for(int k=65;k<=90;k++)
        if(!sum[k]&&flag[k]){
            for(int j=head[k];j!=0;j=e[j].next)
                sum[e[j].y]--;
            ans[now]=k;
            flag[k]=0;//改一下
            dfs(now);
            flag[k]=1;//打扫现场
            for(int j=head[k];j!=0;j=e[j].next)
                sum[e[j].y]++;
        }
}    
int main()
{
    cin>>n>>m;
    memset(l,127,sizeof(l));
    memset(u,127,sizeof(u));
    for(i=1;i<=n;i++)
        for(f=1;f<=m;f++){
            cin>>ch;
            a[i][f]=t=int(ch);
            l[t]=min(f,l[t]);
            r[t]=max(f,r[t]);
            u[t]=min(i,u[t]);
            d[t]=max(i,d[t]);
        }
    for(t=65;t<=90;t++){
        if(r[t]!=0){
            
            f=l[t];
            for(i=u[t];i<=d[t];i++)
                if(a[i][f]!=t)
                    o[t][a[i][f]]=1;
            f=r[t];
            for(i=u[t];i<=d[t];i++)
                if(a[i][f]!=t)
                    o[t][a[i][f]]=1;
            i--;
            for(f=l[t];f<=r[t];f++)
                if(a[i][f]!=t)
                    o[t][a[i][f]]=1;
            i=u[t];
            for(f=l[t];f<=r[t];f++)
                if(a[i][f]!=t)
                    o[t][a[i][f]]=1;
            flag[t]=1;
        }
    }
    n=0;
    for(i=65;i<=90;i++){
        for(f=65;f<=90;f++)
            if(o[i][f])
                sum[f]++,add(i,f);//连边,统计入度
        if(flag[i])//统计总点数n
            n++;
    }
    for(i=65;i<=90;i++){
        if(!sum[i]&&flag[i]){
            for(int j=head[i];j!=0;j=e[j].next)
                sum[e[j].y]--;
            ans[1]=i;
            flag[i]=0;
            dfs(1);//来啊快活啊
            flag[i]=1;//打扫现场
            for(int j=head[i];j!=0;j=e[j].next)
                sum[e[j].y]++;
        }
    }
    return 0;
}

我可能永远也习惯不了这样子的缩进,但还是要努力学习.

让我去吐一会...