平衡二叉树

AVL树学习笔记

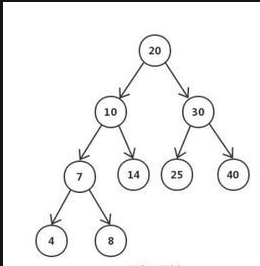
AVL树是带有平衡条件的二叉查找树。

续上文，如果向一棵树输入预先排好序的数据，那么一连串insert操作将花费二次的时间，而链表实现的代价会非常巨大，因为此时的树只由那些没有左儿子的节点组成，一种解决办法，就是要有一颗称为平衡的附加结构条件，任何节点的深度均不得过深。

于是我开始学习一种最古老的平衡查找树，即AVL树。

另外一种较新的方法是放弃平衡条件，允许树有任意的深度，但是在每次操作之后要使用一个调整规则进行调整，使得后面的效率要高，这种类型的数据结构一般属于自调整类型，在二叉查找树的情况下，对于任意的单个操作我们将不再保证o(logN)的时间界，但是可以证明任意连续M次的操作在最坏的情形下花费时间O(M logN)

AVL树的定义

一颗AVL树是其每个节点的左子树和右子树高度最多差1的二叉搜索树(空树的高度定义为-1)

AVL高度探讨

粗略地说，一个AVL树的高度最多为1.44log(N+2)-1.328，但是实际的高度只略大于logN

由插入节点以后AVL树的平衡性可能会遭到破坏，所以我们因此通过对树的操作来维持其平衡性，这就是我们所说的单旋转和双旋转。

我们把必须重新平衡的节点叫做a，由于任意节点最多有两个儿子，因此出现高度不平衡就需要a点的两棵子树的高度差2.

这种不平衡可能出现在下面四种情况中

1 对a的左儿子的左子树进行一次插入

2 对a的左儿子的右子树进行一次插入

3 对a的右儿子的左子树进行一次插入

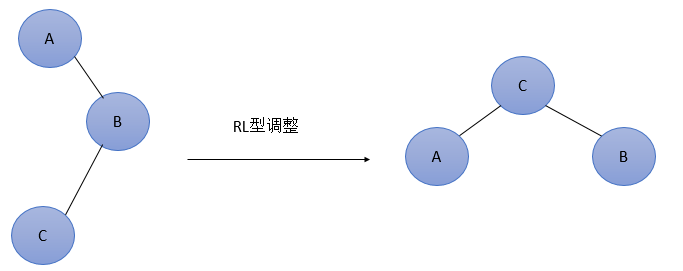
4 对a的右儿子的右子树进行一次插入

情况1和4是关于a点的镜像对称(轴对称)，而2和3是关于a点的镜像对称，因此理论上只有两种情况，当然从编程的角度来看还是四种情形。

第一种情况是插入发生在外边的情况，即左左  右右 的情况，该情况通过对树的一次单旋转而完成调整，第二次情况是插入发生在内部的情形，即左右 右左的情况，该情况需要双旋转来处理。

AVL树实现代码如下

package com.qyx.Tree;
/**
 * 平衡二叉树实现与设计
 * @author QYX
 *
 */
public class AVLTree {
    private static final int ALLOWED_INBALANCE=1;
    private static class AvlNode<AnyType>
    {
        AvlNode left;//左子节点
        AvlNode right;//右子结点
        AnyType element;//元素数据
        int height;//高度
        public AvlNode(AnyType elemet) {
            this(elemet,null,null);
        }
        public AvlNode(AnyType elemet,AvlNode<AnyType> left,AvlNode<AnyType> right) {
            this.element=elemet;
            this.right=right;
            this.left=left;
            this.height=0;
        }
    }
    /*高度计算方法*/
    private int height(AvlNode<Integer> node)
    {
        return node==null?-1:node.height+1;
    }
    /*插入方法*/
    private AvlNode<Integer> insert(Integer x,AvlNode<Integer> node)
    {
        if(node==null)
        {
            return new AvlNode<Integer>(x);
        }
        int compareResult=x.compareTo(node.element);//与其节点的元素值进行比较
        if(compareResult<0)
        {
            node.left=insert(x, node.left);
        }else if(compareResult>0)
        {
            node.right=insert(x,node.right);
        }else{
            ;
        }
        return balance(node);
    }
    /*删除方法*/
    private AvlNode<Integer> remove(Integer x,AvlNode<Integer> node)
    {
        if(node==null)
        {
            return node;
        }
        int compareResult=x.compareTo(node.element);
        if(compareResult<0)
        {
            node.left=remove(x,node.left);
        }else if(compareResult>0)
        {
            node.right=remove(x,node.right);
        }else if(node.left!=null&&node.right!=null)
        {
            //如果要删除的节点左右儿子节点都不为空，则将当前节点的值转换为其右儿子最小节点的值(因为其不能有左儿子)，然后递归删除即可
            node.element=findMin(node.right).element;
            node.right=remove(node.element,node.right);
        }else{
            node=(node.left!=null)?node.left:node.right;
        }
        return null;
    }
    /*寻找最小节点（递归）*/
    private AvlNode<Integer> findMin(AvlNode<Integer> node) {
        if(node==null)
        {
            return null;
        }else if(node.left==null)
        {
            return node;
        }
        return findMin(node.left);
    }
    /*寻找最大节点(非递归)*/
    private AvlNode<Integer> findMax(AvlNode<Integer> node)
    {
        if(node==null)
        {
            return null;
        }
        while(node.right!=null)
        {
            node=node.right;
        }
        return node;
    }
    /*查找该树是否包含某节点*/
    private boolean contains(Integer x,AvlNode<Integer> node)
    {
        if(node==null)
        {
            return false;
        }
        int compareResult=x.compareTo(node.element);
        if(compareResult<0)
        {
            return contains(x, node.left);
        }else if(compareResult>0)
        {
            return contains(x, node.right);
        }else{
            return true;
        }
    }
    /*平衡方法*/
    private AvlNode<Integer> balance(AvlNode<Integer> node) {
        if(node==null)
        {
            return node;
        }
        if(height(node.left)-height(node.right)>ALLOWED_INBALANCE)
        {
            if(height(node.left.left)>=height(node.left.right))
            {
                node=rotateWithLeftChild(node);
            }else{
                node=doubleWithLeftChild(node);
            }
        }else{
            if(height(node.right.right)>=height(node.right.right))
            {
                node=rotateWithRightChild(node);
            }else{
                node=doubleWithRightChild(node);
            }
        }
        node.height=Math.max(height(node.left), height(node.right))+1;
        return node;
    }
    private AvlNode<Integer> doubleWithRightChild(AvlNode<Integer> node) {
        
        node.right=rotateWithLeftChild(node.right);
        return rotateWithRightChild(node);
    }
    private AvlNode<Integer> rotateWithRightChild(AvlNode<Integer> node) {
        AvlNode<Integer> k1=node.right;
        node.right=k1.left;
        k1.left=node;
        node.height=Math.max(height(node.left), height(node.right))+1;
        k1.height=Math.max(height(k1.left), height(k1.right))+1;
        return k1;
    }
    private AvlNode<Integer> doubleWithLeftChild(AvlNode<Integer> node) {
        node.left=rotateWithRightChild(node.left);
        return rotateWithLeftChild(node);
    }
    private AvlNode<Integer> rotateWithLeftChild(AvlNode<Integer> node) {
        AvlNode<Integer> k1=node.left;
        node.left=k1.right;
        k1.right=node;
        node.height=Math.max(height(node.left), height(node.right))+1;
        k1.height=Math.max(height(k1.left), height(k1.right))+1;
        return k1;
    }
    
}