[浅讲]二维前缀和

前缀和，为什么要用前缀和，目的是更方便快捷的使用。我们定义前缀和数组为(sum)，当然一维的前缀和很简单(sum_i)表示在第i个位置（包括的i个位置）前的所有权值的和，即(sum_{j=1}^{i}a_j)

[egin{aligned} sum_i=sum_{i-1}+f_i end{aligned} ]

那么二维前缀和怎么计算呢，我们画个图；

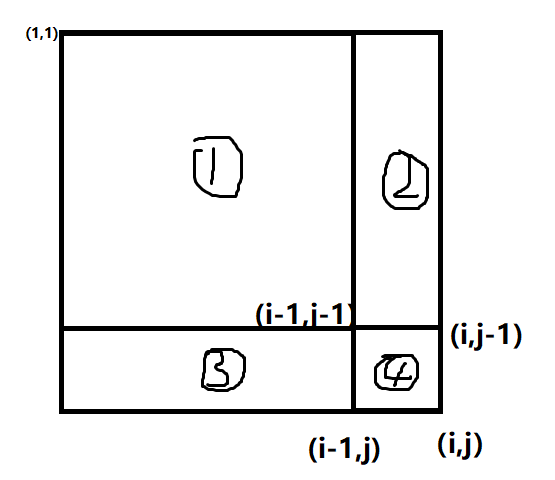
我们定义(sum_{i,j})管辖的区域是①+②+③+④，(sum_{i-1,j})是①+③，(sum_{i,j-1})是①+②，(sum_{i-1,j-1})是①。那么我们思考一下，(sum_{i,j})怎么由(sum_{i-1,j})，(sum_{i,j-1})，(sum_{i-1,j-1})以及这个点的权值（图中的④也就是(f_{i,j})）转换过来呢。我们列出式子：

[egin{aligned} sum_{i,j}=sum_{i-1,j}+sum_{i,j-1}-sum_{i-1,j-1}+f_{i,j} end{aligned} ]

为什么？我们看图，因为(sum_{i-1,j})是①+③，(sum_{i,j-1})是①+②，两个区域相加，是不是重复加了①这个区域所以减掉①，也就是减掉(sum_{i-1,j-1})。没问题吧，然后我们现在拥有了①，②，③三个区域还差一个④，最后加上(f_{i,j})就行了，这样我们就做到了初始化二维前缀和数组。
那么我们怎么计算呢？

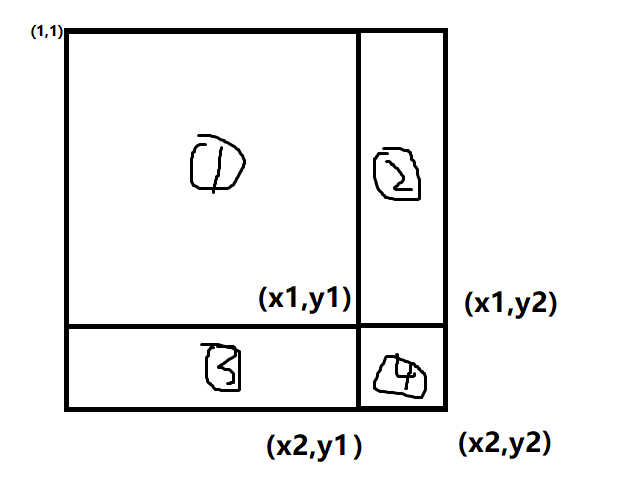
假如我们要求④这个区域的值，也就是像之前一样推演一下就好了

[egin{aligned} sum_{x2,y2}-sum_{x1-1,y2}+sum_{x2,y1-1}+sum_{x1-1,y1-1} end{aligned} ]

给道例题
领地选择

题目描述

作为在虚拟世界里统帅千军万马的领袖，小(Z) 认为天时、地利、人和三者是缺一不可的，所以，谨慎地选择首都的位置对于小 Z 来说是非常重要的。

首都被认为是一个占地 (C imes C) 的正方形。小 Z 希望你寻找到一个合适的位置，使得首都所占领的位置的土地价值和最高。

输入格式

第一行三个整数 (N,M,C)，表示地图的宽和长以及首都的边长。

接下来 (N) 行每行 (M) 个整数，表示了地图上每个地块的价值。价值可能为负数。

输出格式

一行两个整数 (X,Y)，表示首都左上角的坐标。

输入 #1

3 4 2
1 2 3 1
-1 9 0 2
2 0 1 1

输出 #1

1 2

说明/提示

对于 (\%60) 的数据，(N,Mle 50)。

对于 (\%90) 的数据，(N,Mle 300)。

对于 (\%100) 的数据，(1le N,Mle 10^3，1le Cle min(N,M))。

一道模板题吧，就注意下输出的是左上角的坐标，画下图就行了

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e3+10;
int n,m,c;
int sum[maxn][maxn];
int ansx,ansy,maxx=-0x7fffffff;
int main(){
	cin>>n>>m>>c;
	for(int i=1;i<=n;i++)
	 for(int j=1,x;j<=m;j++){
	 	cin>>x;
	 	sum[i][j]=sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1]+x;
	 }
	for(int i=c;i<=n;i++)
	 for(int j=c;j<=m;j++){
	 	if(sum[i][j]+sum[i-c][j-c]-sum[i-c][j]-sum[i][j-c]>maxx){
	 		maxx=sum[i][j]+sum[i-c][j-c]-sum[i-c][j]-sum[i][j-c];
	 		ansx=i,ansy=j;
		 }
	 }
	cout<<ansx-c+1<<" "<<ansy-c+1<<endl;
	return 0;
}