【CCF201412-2】Z字形扫描

试题编号：	201412-2
试题名称：	Z字形扫描
时间限制：	2.0s
内存限制：	256.0MB

问题描述

　　在图像编码的算法中，需要将一个给定的方形矩阵进行Z字形扫描(Zigzag Scan)。给定一个n×n的矩阵，Z字形扫描的过程如下图所示：
　　

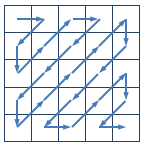
　　对于下面的4×4的矩阵，
　　1 5 3 9
　　3 7 5 6
　　9 4 6 4
　　7 3 1 3
　　对其进行Z字形扫描后得到长度为16的序列：
　　1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3
　　请实现一个Z字形扫描的程序，给定一个n×n的矩阵，输出对这个矩阵进行Z字形扫描的结果。

输入格式

　　输入的第一行包含一个整数n，表示矩阵的大小。
　　输入的第二行到第n+1行每行包含n个正整数，由空格分隔，表示给定的矩阵。

输出格式

　　输出一行，包含n×n个整数，由空格分隔，表示输入的矩阵经过Z字形扫描后的结果。

样例输入

4
1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3

样例输出

1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3

评测用例规模与约定

1≤n≤500，矩阵元素为不超过1000的正整数。

解题报告

题意

给定n×n的矩阵，从左上角开始，按左下右上—右上左下的规律遍历。

思路

一个n×n的矩阵有2n-1条斜线，本题其实就是按照斜线遍历矩阵

我们从左上到右下对2n-1条斜线标号，那么遍历矩阵时，标号为奇数的斜线从左下到右上遍历，标号为偶数的矩阵从右上到左下遍历

以样例为例，遍历过程如下图：

 

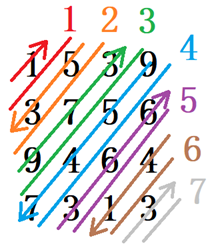
 模拟矩阵的遍历，用i，j表示遍历到矩阵的第i行第j列，即（i，j）

初始时令i=1，j=1，即从矩阵第一条斜线的第一个数开始

由于这条斜线只有一个数，可以直接输出

然后从第二条斜线开始，把剩下2n-2条斜线分组，相邻两条斜线为一组，每一组先遍历标号为偶数的斜线再遍历标号为奇数的斜线，即，每一组先从右上到左下遍历，再从左下到右上遍历

对于右上到左下遍历，下一个位置为（i+1，j-1）

对于左下到右上遍历，下一个位置为（i-1，j+1）

接下来考虑遍历完一条斜线后开始遍历下一条斜线时的过渡

我们注意到，在对角线（即第n条斜线）之前，

标号为奇数的斜线向标号为偶数的斜线过渡时，标号为奇数的斜线的最后一个数在标号为偶数的斜线的第一个数的正左方；

标号为偶数的斜线向标号为奇数的斜线过渡时，标号为偶数的斜线的最后一个数在标号为奇数的斜线的第一个数的正上方

于是我们得到相邻两条斜线过渡的算法

若（i，j）是标号为奇数的斜线的最后一个数，则（i，j+1）过渡到下一条斜线

若（i，j）是标号为偶数的斜线的最后一个数，则（i+1，j）过渡到下一条斜线

同理，我们可以得到对角线后的过渡算法

若（i，j）是标号为奇数的斜线的最后一个数，则（i+1，j）过渡到下一条斜线

若（i，j）是标号为偶数的斜线的最后一个数，则（i，j+1）过渡到下一条斜线

源代码

#include <cstdio>
int n,a[505][505];
int main() 
{
    int i,j;
    scanf("%d",&n);
    for (i=1;i<=n;i++)
      for (j=1;j<=n;j++)
        scanf("%d",&a[i][j]);
    printf("%d",a[1][1]);
    //  直接输出第一个数 
    i=j=1;  //  初始化 
    while (i>=1 && i<=n && j>=1 && j<=n)
    //  确保遍历的位置在矩阵之内 
    //  一次循环为一组遍历 
    {
        //  遍历标号为偶数的斜线 
        if (j<n)  //  当前斜线在对角线之前 
          j++;
        else      //  当前斜线在对角线之后 
          i++;
        if (i>n) break;  
        //  若已经遍历到（n，n）则退出循环
        //  由于只有当j==n时才会执行i++
        //  所以当i>n时j一定已经达到n 
        printf(" %d",a[i][j]);  //  输出第一个数 
        
        while (j>1 && i<n) 
        //  遍历一条斜线 
        {
            i++;   j--;
            printf(" %d",a[i][j]);
        }
        
        //  遍历编号为奇数的斜线 
        if (i<n)  //  当前斜线在对角线之前
          i++;
        else     //  当前斜线在对角线之后 
          j++;
        if (j>n) break;
        printf(" %d",a[i][j]);
        while (i>1 && j<n)
        {
            i--;   j++;
            printf(" %d",a[i][j]);
        }
          
    }
    return 0;
}