Ah 这题 我是被深深地伤害了.....太莫名地TLE了 ==说....
先上题 ~
关于容斥定理 --- 这也是我的处女作
其实这题 一开始 我是想用欧拉函数做的 -> 欧拉函数 一般是计算1~n内与n互质的数的个数 这里的1一般是要根据题目要求来考虑
欧拉函数的 推导过程 真的好麻烦 理解起来好烦 与各种定理一起出现~~
但这题 很特殊 它是问一个区间[l,r]对一个数n 是互质的关系的个数 --- 互质 就是最大公约数是 1
so 我们要换种方法 使用一个叫容斥原理的东西..
它的思想:from百度:
先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
这里 我们首先为了方便计算 将[ l , r ] 对n的互质的个数通过 [ 1 ,r ] - [ 1 , l-1 ] 来求得
求互质 我们可以用逆向思维来做 找出非互质的 即最大公约数 >1的数X 然后总数SUM来 减去 这个X 即Y=互质数
每个合数 都可以用 质数的 乘积来表示 如 12 = 2 *2*3 10 = 2*5 8 = 2*2*2 …………
你可以看到 12 10上的最大公约数是2 因为他们含有共同的 质因子2 这边 其实 我们并不需要刻意去求出 它们的最大公约数 只要证明2者之间有非1的质因子就可以
那么 我们首先预处理n 求出它有哪些 质因子 存储到一个数组中去
然后 我们假设 它有 2 3 5这3个质因子
那么 你也看到了 容斥原理 是先将它的所有组合方案求出来 这边的数量当然是7 即 2 3 5 (2,3),(2,5),(3,5),(2,3,5)
接下去 对于每个方案的处理是最关键的 用了很cool的二进制来实现 因为二进制 每位上是0或1 这里一旦有一位上出现1 我们就表示 这里有一个质因子出现 我这边为了更明了 我将1~7 各自的二进制 全给写出来 001 010 011 100 101 110 111 你可以看到 以每个二进制为考虑对象 一共出现3个(1个1) 3个(2个1) 1个(3个1) 完美对应上面方案的质因子数
那你可能会想 --- 怎么去判断0 1位呢? 我们通过很神奇的 & 来实现---2位都是1 才是1
这个 我会在 == 的代码里 我觉得这边 自己分析不好 就不写了~~
然后 最后讲下 应该刚刚介绍 容斥原理时就应该讲的一个公式
S(AuBuC) = S(A)+S(B)+S(C)-S(A∩B)-S(B∩C)-S(C∩A)+S(A∩B∩C)
这里的A B C各自表示一个集合.. 嗯 我去画个图 就好理解了~
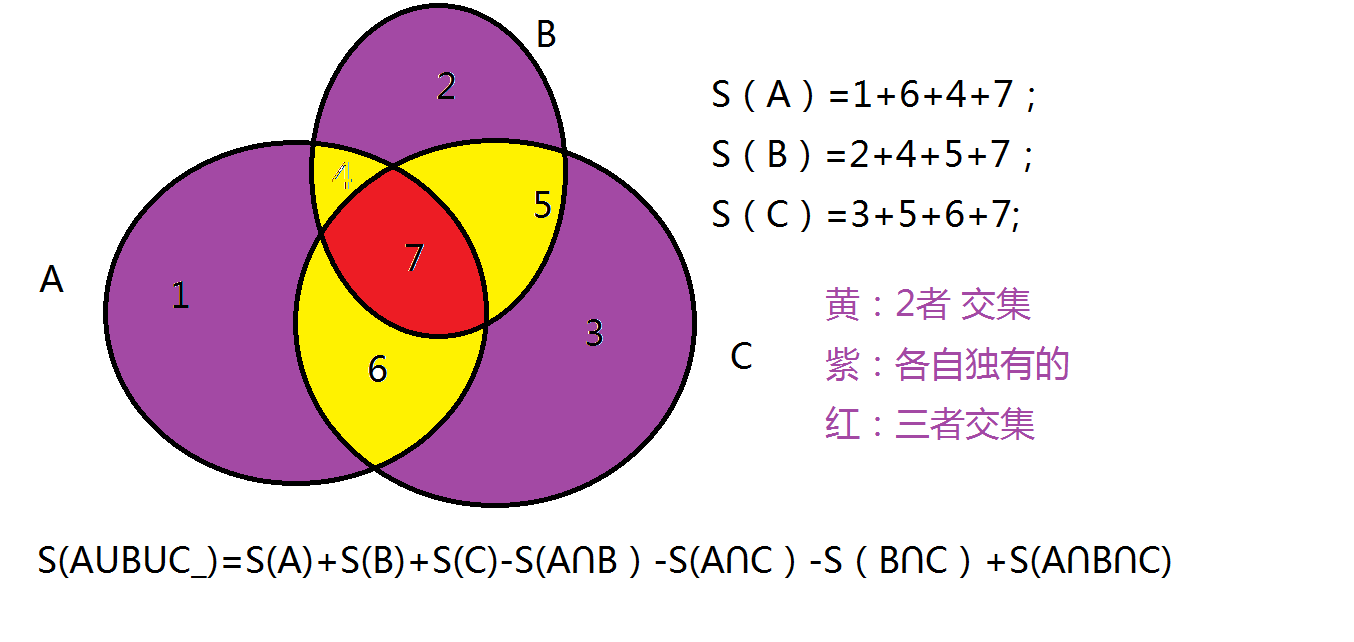
这边 我分开区域 只是为了当你和我起初一样 第一次接触的时候 更好理解嘛~
最后 讲一个被深深打击的地方了
我在TOJ上Long long 用 lld TLE 使用 I64d AC =-=
感谢 看完 又臭又长的叙述 ~ 最后 贴 代码

1 #include <iostream> 2 using namespace std; 3 4 #define LL long long 5 const int size = 10100; 6 int fact[size]; 7 LL slove (LL n, LL r) 8 { 9 int cnt = 0; 10 for (int i=2; i*i<=n; ++i) 11 { 12 if (n % i == 0) 13 { 14 fact[cnt++] = i; 15 while (n % i == 0) 16 n /= i; 17 } 18 }// 这个 for 就是查找传入的参数 n 有哪些质因子 因为while的存在 所以 fact数组内存的数肯定都是质数且都是n的因子 19 if (n > 1) 20 fact[cnt++] = n; // 这里n 未除尽 添入数组 21 LL sum = 0; 22 for (int msk=1; msk < ( 1<<cnt ) ; ++msk) //这边 1<<cnt 是指如果这里有 2 3 5这3个质因子 那么可以构成2 3 5 (2,3),(2,5),(3,5),(2,3,5)这7种情况 所以循环是[1,8) 23 { 24 int temp = 1; // 这就是 存储下面的 fact[i]的并且实现累乘 25 int var = 0; 26 for (int i=0; i<cnt; ++i ) 27 { // 这边 相当于将二进制每个下标为1时 看成1个质因子的存在 如0010 0100是存在一个 0110 存在2个 1110存在3个.. 28 if ( msk & (1<<i) ) // 通过 & 操作 来确定是几个质因子 进行计算 29 { // 如当 msk = 2 cnt = 3时 2&1 = 0 2&2 = 1 2&4 = 0可以看出只有一个因子进行了计算 2的二进制->010 30 ++var; // 当 msk = 3 cnt = 3时 3&1 = 1 3&2 = 1 3&4 = 0可以看出有2个因子进行了计算 3的二进制->011 符合上面提到的 31 temp *= fact[i]; 32 } 33 } 34 LL cur = r / temp; // 计算是 此时 乘积 的倍数的个数为多少 35 if ( var % 2 == 1 ) // 这里应该是根据 S(AuBuC) = S(A)+S(B)+S(C)-S(A∩B)-S(B∩C)-S(C∩A)+S(A∩B∩C)来判断 看括号里有几个数判断+-符号 36 sum += cur; 37 else 38 sum -= cur; 39 } 40 return r - sum;//因为sum求出的是整除这些质数的数 我们要求的是与n互质 所以减去 41 } 42 43 int main() 44 { 45 int t; 46 LL l , r , n; 47 while( ~scanf("%d",&t) ) 48 { 49 for( int i = 1 ; i<=t ; i++ ) 50 { 51 scanf( "%lld %lld %lld",&l,&r,&n ); 52 printf( "Case #%d: %lld ",i,slove(n,r)-slove(n,l-1) );// 分别计算[1,R]与[1,L-1]来相减.------l 1真的好难区分 53 } 54 } 55 return 0; 56 }
