最近遇到好多优先队列的题啊 今天cf的B就是 优先队列的..如果我终测 是AC的话..
这题 的普通做法话 是用优先队列来做 很多人 也都是这样做的
但我在discuss里看到了 用dp的决策背包去做 这种思想特别好我这边 讲下它的思路 至于优先队列的就懒得说喽.
这边有段代码 特别核心 而且以后我们也可以拿来用 好像我自己还未用过
1 j=cnt=0,k=n;; 2 while(cnt<q) 3 { 4 cnt+=k; 5 j++; 6 if (j==n) 7 break; 8 k=(k*(n-j)/(j+1)); 9 }
就是说 最后得到的是 在q<=所有的组合数的情况下
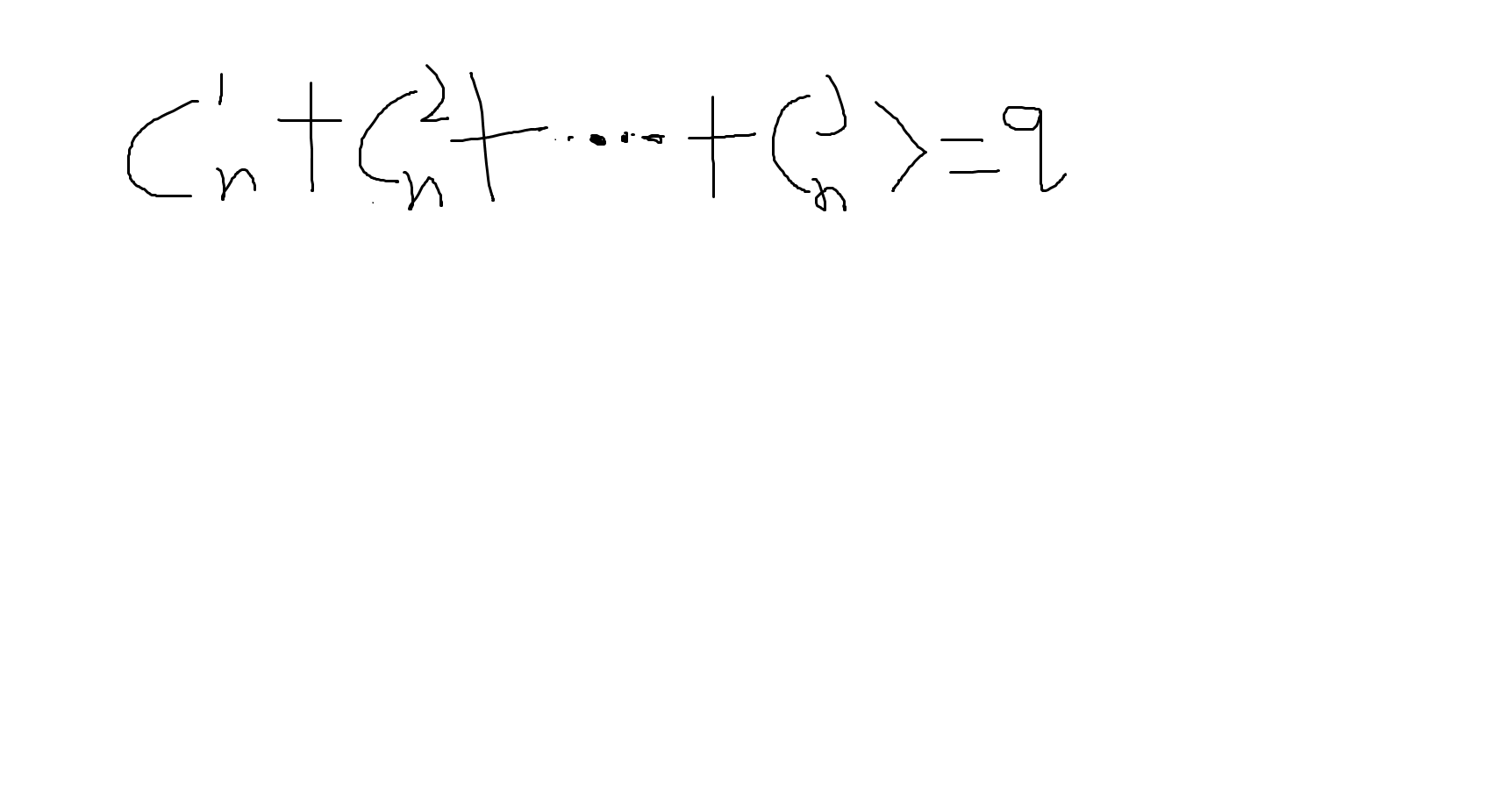
>=的前面是字母j
1 for (m=0,i=n-1;j!=0;j--) 2 m+=a[i--];
所以这边 就是找出最坏的情况下 取出j道题目的最大难度
1 memset(f,0,sizeof(f)); 2 f[0] = 1;//我修改的 3 for (i=0;i<n;i++) 4 { 5 for (j=m;j-a[i]>=0;j--) 6 {//if (f[j-a[i]])原作者写的 7 f[j] += f[j-a[i]]; 8 //f[a[i]]++;原作者写的 9 } 10 } 11 f[0] = 0;//我修改的
这里 可以将它看成个01背包 f[x]数组的定义是 难度<=x的方案数有多少个
当然 在上述代码中 我们只能求出f[x]当难度恰好为x时候的方案数
不过没关系 我们只要在上述代码执行完毕后 遍历1-m用递推来累加就可以了
1 for (i=1;i<=m;i++) 2 f[i]+=f[i-1];
然后 你可以对比下 我的写法 和 原先作者的写法 我们只是在初始化上有点不同而已
其实 仔细想想 会发现我的程序 有个Bug 就是默认了 输入的难度 没有0的存在 ..
然后 我去和Hdu的admin要了数据..本来抱着试一试的希望 没想到 很快就给我了数据 不得不提下 很感谢
然后 他们的数据里 就是有0 而且不止一组 -.-

1 #include <iostream> 2 #include <queue> 3 #include <algorithm> 4 using namespace std; 5 6 int n , m; 7 typedef long long LL; 8 const int size = 11010; 9 LL arr[size]; 10 struct node 11 { 12 LL sum; 13 LL nextSum; 14 int nextId; 15 node(){}; 16 node( LL a , LL b , int c ):sum(a),nextSum(b),nextId(c){}; 17 bool operator < ( const node & q )const 18 { 19 return nextSum > q.nextSum;//小的先出队 20 } 21 }; 22 priority_queue<node> q; 23 24 LL solve( ) 25 { 26 while( !q.empty() ) 27 q.pop(); 28 q.push( node(0 , arr[0] , 0) ); 29 int cnt; 30 LL ans , var; 31 node now; 32 cnt = arr[n] = 0; 33 while( cnt<m ) 34 { 35 now = q.top(); 36 q.pop(); 37 var = now.nextSum; 38 if( now.nextId>=n ) 39 { 40 continue; 41 } 42 q.push( node( now.sum , now.sum+arr[ now.nextId+1 ] , now.nextId+1 ) ); 43 q.push( node( now.nextSum , now.nextSum+arr[ now.nextId+1 ] , now.nextId+1 ) ); 44 ++ cnt; 45 } 46 return var; 47 } 48 49 int main() 50 { 51 cin.sync_with_stdio(false); 52 int t; 53 cin >> t; 54 LL ans; 55 for ( int k = 1 ; k<=t ; ++k ) 56 { 57 cin >> n >> m; 58 for ( int i = 0 ; i<n ; ++i ) 59 { 60 cin >> arr[i]; 61 } 62 sort( arr , arr+n ); 63 ans = solve( ); 64 cout << "Case #" << k << ": " << ans << endl; 65 } 66 return 0; 67 }
贴下 优先队列的代码 至于那个背包的 就懒得贴了 可以去discuss里面看到
today:
有时
你期待一切如新
有时
你期待一切如常
有时
你期待一切如旧
但是
过去与未来现在都去不了
