在这里需要说明一点,任何领域的概念、技术都有其特定的适用范围,有其解决的问题,有其发展的历史,所以,抛开应用环境、范围来谈技术就像是没有根系的枝丫,枝丫再粗壮也只是一根木头而已。
那接下来我们来聊聊什么是GIS的数学基础。下面就以解决问题的思路来说明。
1. 引子
GIS有多种理解方式:从一个角度来讲,它是一个处理空间信息的工具,所谓空间信息是和人们相关的一些要素(feature这个词不太好解释,可以理解为"东西")的位置、及其相互关系。
位置(position),描述这个要素在地球的什么地方;
关系(resolution),描述的这些要素之间的相对位置及相互影响的方式。
谈到位置,我们需要建立一系列的标准来定义它,而这一系列的标准就是GIS的数学基础,也称作地理参考系统,比如,地球是什么样的?怎么描述她?位置如何来描述?怎么去解决地球是椭球体,而一般的阅读载体是平面这个问题?
2. 这些标准有哪些
下面用一张简图来说明这些概念及其关系
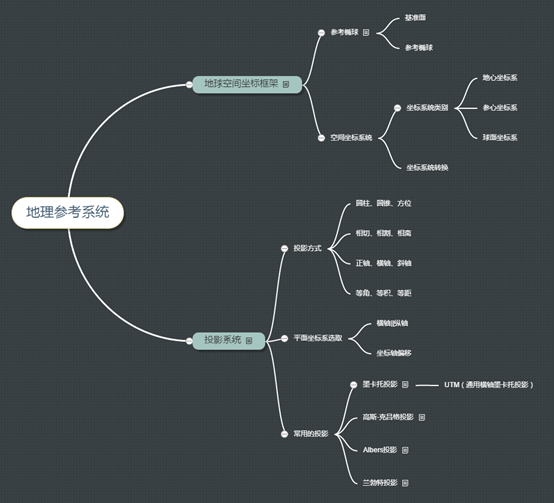
2.1 空间坐标框架
以数字形式来描述地球及其上面的物体,需要一个基准,所有的物体在这个基准上都可以有特定位置。
空间坐标框架就是解决这样的问题的,它需要解决的问题有两个,1是地球是如何描述的,它的数学模型是什么样的?2是要说明与人相关的要素(feature)就应该有一个参照的系统,在这个参照系统下每个点的位置是如何定义的;上面这两个问题也就是1参考椭球,2空间坐标系。
① 参考椭球
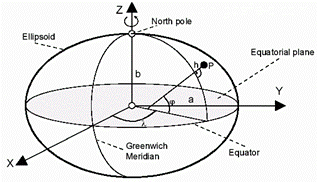
■ 什么是参考椭球?
地球是一个极度不规则的球体,高的地方平均海拔在4000m以上(青藏高原),低的地方平均深度为-6000m以上(马里亚纳海沟),但是为了便于描述,从一定程度上对地球进行简化描写,可以用一个特定的椭球来代表地球(如上图),这个特定的椭球就是参考椭球。
■ 数学意义的参考椭球?
数学意义的参考椭球是用一定参数来确定的
-
椭球方程 x²/a²+y²/b²+z²/c²=1
-
椭球方程参数 半长径(a)、半短径(b)、扁率(e)
例,1980年国际大地测量与地球物理联合会推荐参数:半长径a=6378137;半短径b=6356752;扁率e=(a-b)/a=1:298.257
随着近代科学技术的发展,人类对地球的认识也在发生着变化,在不同的时期,都会存在着一些当前时期比较精准的椭球体,例如,卡拉克椭球,卡拉索夫斯基椭球,WGS84椭球等。
② 空间坐标系
■ 什么是空间坐标系
一般所说的空间坐标系都是有着特定的坐标原点,特定三维坐标轴定义的坐标系(如下图,空间直角坐标系)。这样可以描述一个物体的前、后、左、右、上、下等关系。
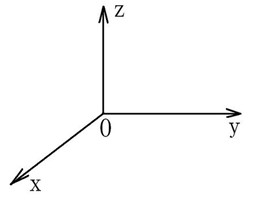
■ 有哪些空间坐标系?
根据坐标定义的不同可以分为:空间直角坐标系,空间大地坐标系。
空间直角坐标系
这个坐标系在地理学中一般不常用。它的定义比较简单,以参考椭球的球心为原点,Z轴指向北极,X轴指向起始子午面与赤道的交点,Y轴位于赤道面上切按右手系于X轴呈90度夹角。
这个坐标系中的某个点坐标可用该点在此坐标系的各个坐标轴上的投影来表示。如下图:

空间大地坐标系
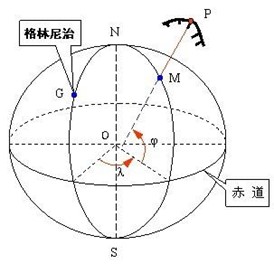
这是常用的经纬度的坐标系定义。大地纬度、经度和大地高程来描述空间位置的。
纬度是空间的点与参考椭球面的法线与赤道面的夹角;
经度是空间的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角;
大地高程是空间的点沿着参考椭球的法线方向到参考椭球面的距离。
根据坐标系原点的不同可以分为:地心坐标系,参心坐标系
地心坐标系(geocentric coordinate system)
有两种情况:一是坐标系原点在地球质心的空间直角坐标系;二是球心与地球质心重合的参考椭球面为基准建立的空间大地坐标系。
参心坐标系(reference-ellipsoid-centric coordinate system)
同样有两种情况:一是坐标系原点在参考椭球的几何中心的空间直角坐标系;二是坐标系原点在参考椭球的几何中心的空间大地坐标系。
球面坐标是另外一种描述位置的方法,具体可以访问这个链接[百度百科:球面坐标系]
2.2 投影系统
■ 解决的问题?
地球是个椭球体,而我们一般的阅读媒介都是平面的,那如何来实现从椭球体到平面的转换呢?投影系统的目的就是解决这个问题。
其实投影是一种方法,把椭球上的点映射到平面上的方法。这种方法一般包括3个方面:选择哪个参考椭球?选择投影到哪种平面上?使用什么样的映射方式?
总体来说:投影=2种媒介+1种映射方式。
■媒介1:参考椭球
已经在上面有描述了,无非就是选择一个参考椭球。
■媒介2:平面
平面比较好理解,一个平整的面,可以是其他物体上展开的平面,比如圆柱体侧面,圆锥体侧面等。
在这儿需要注意的是平面坐标系的选取:原点的如何确定?X轴和Y轴如何定义?当然一般都是右手坐标系。
■ 映射方式?
① 根据投影面的不同,有以下几种投影方式:
投影到圆柱体上,再把圆柱体面展开形成平面,叫做圆柱投影
投影到圆锥体上,再把圆锥体面展开形成平面,叫做圆柱投影
直接投影到平面上叫做方位投影。
② 根据投影面与参考椭球的位置关系,分以下几种投影方式:
相切、相隔、相离
③ 根据投影面的轴与参考椭球的自转轴的位置关系,分为以下几种投影方式:
正轴、横轴、斜轴
④ 根据投影后图形与原参考椭球上的图形的关系,分为以下几种投影方式:
等面积、等角度、等距离
■ 常用的投影
① 墨卡托投影(正轴等角切圆柱投影)
投影方式:假设地球被围在一中空的圆柱里,其基准纬线与圆柱相切(赤道)接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅选定基准纬线上的"墨卡托投影"绘制出的地图
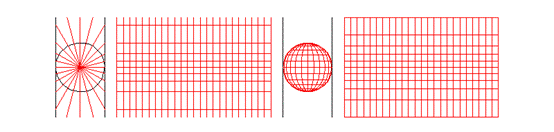
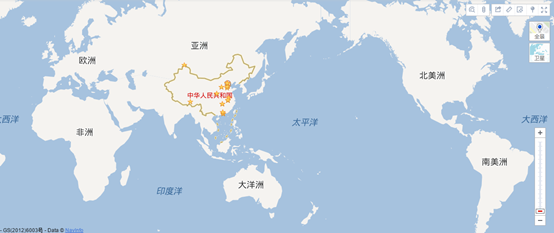
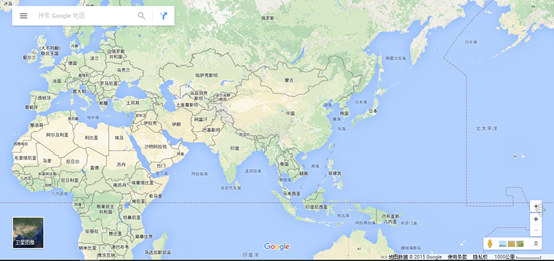
投影用途:世界地图
例如,百度地图,Google 地图
② 高斯-克吕格投影(横轴等角切椭圆柱投影)
投影方式:
假设一个椭圆柱面与地球椭球体面横切于某一条经线上,按照等角条件将中央经线东、西各3°或1.5°经线范围内的经纬线投影到椭圆柱面上,然后将椭圆柱面展开成平面而成
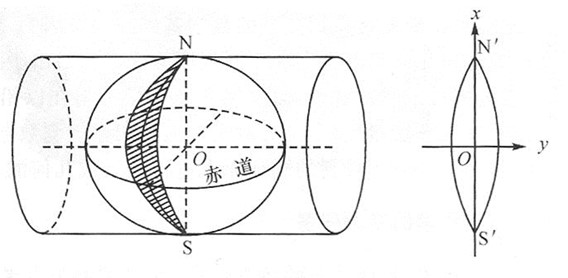
投影用途:我国大比例尺地形图
我国各种大、中比例尺地形图采用了不同的高斯-克吕格投影带。其中大于1:1万的地形图采用3°带;1:2.5万至1:50万的地形图采用6°带。
③ Albers投影(双标准纬线等积割圆锥投影)
投影方式:将参考椭球北极向上置于圆锥面中心,并突出于圆锥面,使圆锥面与参考椭球有两个交线(纬线),以参考椭球中心点向外发光的方式照射于圆锥面上,并将圆锥面展开。
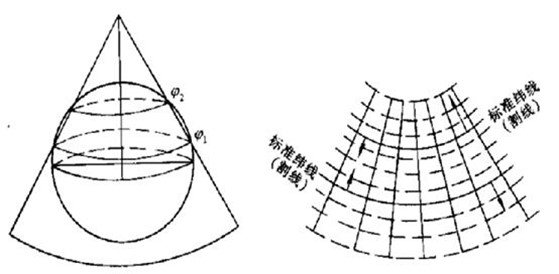
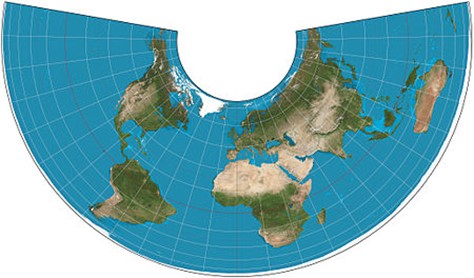
投影用途:我国小比例尺(400万,100万)地图使用的投影,如行政区划图