7.26 搜索进阶（状压搜索，迭代加深搜索）

状压搜索   广搜

用广搜好保存状态（钥匙）对钥匙的状态进行状态压缩，每一个位置上1或0对应有没有这种钥匙

C题：

AveryBoy又又又被关在一个n*m的迷宫里，这次还有了检查人员防止他逃跑。，并在迷宫的某些地方安装了带锁的门，钥匙藏在迷宫另外的某些地方。刚开始AveryBoy被关在(sx,sy)的位置，离开迷宫的门在(ex,ey)的位置。AveryBoy每分钟只能从一个坐标走到相邻四个坐标中的其中一个。检查人员每t分钟回地牢视察一次，若发现AveryBoy不在原位置便把他拎回去。经过若干次的尝试，AveryBoy已画出整个迷宫的地图。现在请你帮他计算能否再次成功逃出迷宫。只要在检查人员下次视察之前走到出口就算离开迷宫，如果检查人员回来的时候刚好走到出口或还未到出口都算逃亡失败。

Input

每组测试数据的第一行有三个整数n,m,t(2<=n,m<=20,t>0)。接下来的n行m列为迷宫的地图，其中包括:

. 代表路
* 代表墙
@ 代表AveryBoy的起始位置
^ 代表地牢的出口
A-J 代表带锁的门,对应的钥匙分别为a-j
a-j 代表钥匙，对应的门分别为A-J

每组测试数据之间有一个空行。

Output

针对每组测试数据，如果可以成功逃出迷宫，请输出需要多少分钟才能离开，如果不能则输出-1。

Sample Input

4 5 17
@A.B.
a*.*.
*..*^
c..b*

4 5 16
@A.B.
a*.*.
*..*^
c..b*

Sample Output

16
-1

#include<bits/stdc++.h>
using namespace std;
char maze[25][25];
bool vis[25][25][1200];
int sx,sy,ex,ey,t,n,m;
int cnt;
int nx[4]={1,0,0,-1};
int ny[4]={0,1,-1,0};
struct node
{
    int x,y,key,step;
}st;
bool check(node temp)
{
    if(temp.x<0||temp.x>=n||temp.y<0||temp.y>=m)return false;
    else if(maze[temp.x][temp.y]=='*'||vis[temp.x][temp.y][temp.key])return false;
    else return true;
}
void bfs()
{
    node tmp,next;
    queue<node>que;
    que.push(st);
    vis[sx][sy][0]=true;
    while(!que.empty())
    {
        tmp=que.front();
        que.pop();
        for(int i=0;i<4;i++)
        {
            next=tmp;
            next.x+=nx[i];
            next.y+=ny[i];
            next.step++;
            if(next.step>=t)return;    //剪枝，若消耗时间已经>=t但还没有走到终点，则不可能逃离迷宫；
            if(check(next))
            {
                if(next.x==ex&&next.y==ey)
                {
                   if(next.step<t)cnt=next.step; //最先找到的一定最优，满足条件才给cnt赋值
                   return;
                }
                else if(maze[next.x][next.y]=='.')
                {
                    vis[next.x][next.y][next.key]=true;
                    que.push(next);
                }
                /*else if(next.x==sx&&next.y==sy)
                {
                    if(!vis[next.x][next.y][next.key])
                    {
                        vis[next.x][next.y][next.key]=true;
                        que.push(next);
                    }
                }*/
                else if(maze[next.x][next.y]>='A'&&maze[next.x][next.y]<='J') //碰到了门
                {
                    int flag=(next.key>>(maze[next.x][next.y]-'A'))&1;  //对钥匙状态压缩，看每个位置有没有门对应编号的钥匙
                    if(flag)
                    {
                        vis[next.x][next.y][next.key]=true;
                        que.push(next);
                    }
                }
                else //碰到了钥匙
                {
                    next.key=next.key|(1<<(maze[next.x][next.y]-'a'));//对手里钥匙的状态进行更新
                    if(!vis[next.x][next.y][next.key])   //看更新钥匙之后的这个位置有没有出现过；
                    {
                        vis[next.x][next.y][next.key]=true;
                        que.push(next);
                    }
                }
            }
        }
    }
    return;
}
int main()
{
    while(~scanf("%d%d%d",&n,&m,&t))
    {
      int i,j;
      cnt=-1;
      for(i=0;i<n;i++)scanf("%s",maze[i]);
      for(i=0;i<n;i++)
      {
          for(j=0;j<m;j++)
          {
               if(maze[i][j]=='@')
            {
                sx=i;
                sy=j;
                st.x=sx;
                st.y=sy;
                st.key=0;
                st.step=0;
                maze[i][j]='.';//将起点置为“可走”，接下来就不用特判
            }
            if(maze[i][j]=='^')
            {
                ex=i;
                ey=j;
            }
          }
      }
       memset(vis,false,sizeof vis);
       bfs();
       printf("%d
",cnt);
    }
    return 0;
}

所谓迭代加深搜索：

就是限制DFS的深度，若搜不到答案，则加深深度，重新搜索，这样就防止了随着深度不断加深而进行的盲目搜索，而且，对于这种求最短长度之类的题目，只要找到可行解，即是最优解了。同时注意剪枝，每次DFS的时候，都要判断一下，当前的深度＋最少还有加深的深度是否大于限制的长度，若是，则退回上一层状态。

A题：

迭代加深搜索

AveryBoy最近迷上了旋转游戏。旋转游戏使用＃形板，可以容纳24块方块（见图）。这些块标有数字1,2和3，每种正好有8个。

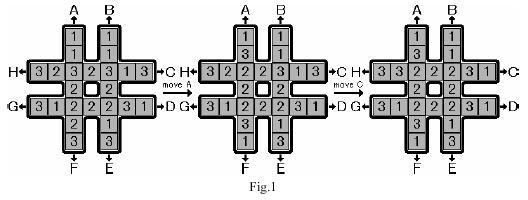
最初块随放在板子上，你的目标是移动块，使放置在中心方块的八个块具有相同的符号标记。只有一种类型的有效移动，即旋转四条线中的一条，每条线由七个块组成。也就是说，线中的六个块向头部移动一个块，并且头块移动到线的末端。八个可能的移动用大写字母A到H标记。图示出了两个连续的移动，移动A和移动C。

Input

输入包含不超过30个测试用例。每个测试用例只有一行包含24个数字，这些数字是初始配置中块的符号。块的行从上到下列出。对于每一行，块从左到右列出。数字用空格分隔。例如，样例输入中的第一个测试用例对应于图中的初始配置。案件之间没有空行。在结束输入的最后一个测试用例之后，有一行包含单个“0”。

Output

对于每个测试用例，您必须输出两行。第一行包含达到最终配置所需的所有动作。每个动作都是一个字母，从“A”到“H”，并且行中的字母之间不应有任何空格。如果不需要移动，则输出“No moves needed”。在第二行中，您必须在这些移动后输出中心方块中的块数字。如果有多种可能的解决方案，则必须输出使用最少移动次数的解决方案。如果仍有多个可能的解决方案，则必须输出字典顺序中最小的解决方案。不需要在案例之间输出空行。

Sample Input

1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3
1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
0

Sample Output

AC
2
DDHH
2

https://lo-li.net/1363.html#comment-737

#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
const int indexs[8][7] =
 {                        // 每种操作变动的下标
    { 0,2,6,11,15,20,22 },    //AF
    { 1,3,8,12,17,21,23 },    //BE
    { 10,9,8,7,6,5,4 },       //CH
    { 19,18,17,16,15,14,13 }, //DG
    { 23,21,17,12,8,3,1 },    //EB
    { 22,20,15,11,6,2,0 },    //FA
    { 13,14,15,16,17,18,19 }, //GD
    { 4,5,6,7,8,9,10 },       //HC
};
const int reverseop[] = { 5,4,7,6,1,0,3,2,-1 }; // A-H的逆操作
const int center[] = { 6,7,8,11,12,15,16,17 };   // 中心八点下标
int maze[24];
char route[101];                                 // 操作序列
bool flag;
void pull (int op)
{
    int temp=maze[indexs[op][0]];
    for(int i=0;i<6;i++)
    {
        maze[indexs[op][i]]=maze[indexs[op][i+1]];
    }
    maze[indexs[op][6]]=temp;
}
int geth()
{
    int cnt[3]={0,0,0};
    int maxcnt=-1;
    for(int i=0;i<8;i++)
    {
        cnt[maze[center[i]]-1]++;
        maxcnt=max(maxcnt,cnt[maze[center[i]]-1]);
    }
    return 8-maxcnt;
}
void dfs(int depth,int lastop,int maxdepth)
{
    if(flag)return;
    if(geth()==0)
    {
        flag=true;
        route[depth]='';
        printf("%s
%d
",route,maze[center[0]]);
        return;
    }
    if(depth>maxdepth||geth()+depth>maxdepth)return;
    for(int nextop=0;nextop<8;nextop++)
    {
        if(nextop!=reverseop[lastop])
        {
            pull(nextop);
            route[depth]=nextop+'A';
            dfs(depth+1,nextop,maxdepth);
            pull(reverseop[nextop]);
        }
    }

}
int main()
{
    while(1)
    {
        int i;
        for(i=0;i<24;i++)
        {
            scanf("%d",&maze[i]);
            if(maze[i]==0)return 0;
        }
        flag=false;
        if(geth()==0)
        {
            printf("No moves needed
%d
",maze[center[0]]);
            continue;
        }
        else
        {
            for(int depth=1;!flag;depth++)
            {
                dfs(0,8,depth);
            }
        }
    }
    return 0;
}

B题：

 迭代加深搜索

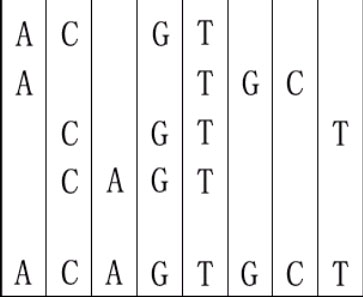
二十一世纪是生物技术发展的世纪。我们知道基因是由DNA组成的。构建DNA的核苷酸碱基是A（腺嘌呤），C（胞嘧啶），G（鸟嘌呤）和T（胸腺嘧啶）。给定几个DNA序列，要求您从它们中制作一个最短的序列，以便每个给定的序列是它的子序列。

例如，给定“ACGT”，“ATGC”，“CGTT”和“CAGT”，您可以按以下方式制作序列。它是最短的但可能不是唯一的。

Input

第一行是测试用例编号t。然后是t组测试用例。在每种情况下，第一行是整数n（1 <= n <= 8）表示DNA序列的数目。以下n行包含n个序列，每行一个。假设任何序列的长度在1到5之间。

Output

对于每个测试用例，打印一行，表示可以从这些序列中生成的最短序列的长度。

Sample Input

1
4
ACGT
ATGC
CGTT
CAGT

Sample Output

8

#include <bits/stdc++.h>
using namespace std;
char str[10][10];
int n,ans;
int deep;
char DNA[4]={'A','G','C','T'};//四种可能
void dfs(int depth,int len[]) //len[j]就是对于第j个字符串当前已匹配到的长度
{
    if(depth>deep)return;//大于限制的深度，不用往下搜索
    int i,j,maxx=0;
    for(i=0;i<n;i++)
    {
        int l=strlen(str[i])-len[i];//预计还要匹配的最大长度
        maxx=max(l,maxx);
    }
    if(maxx==0)
    {
        ans=depth;//已经匹配完了，条件都已满足，当前搜索（操作）次数即是答案
        return;
    }
    if(depth+maxx>deep)return;//如果当前搜索深度+最少还要加深的深度>限制的深度，退回
    for(i=0;i<4;i++)//这个深度有四种放置选择
    {
        int flag=0;   
        int pos[10];  //对于每一个字符串已经匹配到的长度；
        for(j=0;j<n;j++)//遍历n个字符串
        {
            if(str[j][len[j]]==DNA[i])//如果这个字符串当前匹配到的位置的元素与我的选择匹配了
            {
                flag=1;//我这个选择是对的
                pos[j]=len[j]+1;//这个字符串匹配的长度+1；
            }
            else pos[j]=len[j];
        }
        if(flag)dfs(depth+1,pos);//如果我这个选择是对的，那么进行下一深度的搜索
        if(ans!=-1)return;//已搜到最优解，不用往下进行
    }
}
int main()
{
    int t,i;
    cin>>t;
    while(t--)
    {
        scanf("%d",&n);
        int maxn=-1;
        for(i=0;i<n;i++)
        {
            scanf("%s",str[i]); //字符串输入应该这样写
            int l=strlen(str[i]);
            maxn=max(maxn,l);
        }
        deep=maxn; //最小长度至少为序列里长度最大的那一个
        ans=-1;
        int pos[10]={0};  //pos数组用来存放从0号到n-1号字符串已经匹配到的长度；
        while(1)
        {
            dfs(0,pos);//每次都从深度0开始搜索，一直搜到限制值
            if(ans!=-1)break;
            deep++;//没有找到最优解，搜索限制+1
        }
        printf("%d
",ans);
    }
    return 0;
}