hdu 6397 charactor encoding

Character Encoding

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 1692    Accepted Submission(s): 650

Problem Description

In computer science, a character is a letter, a digit, a punctuation mark or some other similar symbol. Since computers can only process numbers, number codes are used to represent characters, which is known as character encoding. A character encoding system establishes a bijection between the elements of an alphabet of a certain size n and integers from 0 to n−1. Some well known character encoding systems include American Standard Code for Information Interchange (ASCII), which has an alphabet size 128, and the extended ASCII, which has an alphabet size 256.

For example, in ASCII encoding system, the word wdy is encoded as [119, 100, 121], while jsw is encoded as [106, 115, 119]. It can be noticed that both 119+100+121=340 and 106+115+119=340, thus the sum of the encoded numbers of the two words are equal. In fact, there are in all 903 such words of length 3 in an encoding system of alphabet size 128 (in this example, ASCII). The problem is as follows: given an encoding system of alphabet size n where each character is encoded as a number between 0 and n−1 inclusive, how many different words of length m are there, such that the sum of the encoded numbers of all characters is equal to k?

Since the answer may be large, you only need to output it modulo 998244353.

 

Input

The first line of input is a single integer T (1≤T≤400), the number of test cases.

Each test case includes a line of three integers n,m,k (1≤n,m≤105,0≤k≤105), denoting the size of the alphabet of the encoding system, the length of the word, and the required sum of the encoded numbers of all characters, respectively.

It is guaranteed that the sum of n, the sum of m and the sum of k don't exceed 5×106, respectively.

 

Output

For each test case, display the answer modulo 998244353 in a single line.

 

Sample Input

4 2 3 3 2 3 4 3 3 3 128 3 340

 

Sample Output

1 0 7 903

 

 

 

题意：

x1+x2+x3+...xm=k, 0<=xi<=n-1,已知n,m,k，求所有可能的情况数。

 

解法：

如果这个题xi没有上限，那么就是一个把k个1（小球）放到m个盒子里，允许空盒的情形，采用隔板法，先将每个盒子里先放上一个球，那么现在共有m+k个球，形成了m+k-1个间隙，在这些间隙中选出m-1个间隙放上隔板，即可将这些小球（1）分成m份，也就是让这些1形成了m个数。

现在xi存在上限

假设我们先从总和m+k中选出n个球放在一边，然后把剩余的m+k-n个球分到m个盒子中，接着再把预先选出的n个球放到这m个盒子中的任意一个中，此时这个被选中的盒子里的球数肯定是大于等于n的，也就是说这种情况至少有1个盒子里的球是超出限制的。

同理我们选出2*n个球放一边...这种情况至少有2个盒子里的球是超出限制的。

......

我们最多选到(k/n)*n个球放一边，此时至少有k/n个盒子超出限制。

因为每个事件存在重叠的部分，所以用到容斥原理

总的情况数为

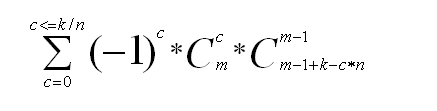
注意要预处理阶乘以及阶乘的逆元

AC代码：

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mod=998244353;
const int maxn=2e5+10;
ll  fac[maxn],invfac[maxn],inv[maxn];  //fac[i]代表i的阶乘，invfac[i]代表i阶乘的逆元
void init()
{
    inv[1]=1;
    int i;
    for(i=2;i<maxn;i++)
    {
        inv[i]=(mod-mod/i)*inv[mod%i]%mod;//求逆元
    }
    fac[0]=1;
    invfac[0]=1;
    for(i=1;i<maxn;i++)
    {
        fac[i]=fac[i-1]*i%mod;//求阶乘
        invfac[i]=invfac[i-1]*inv[i]%mod;//求阶乘的逆元
    }
}
ll C(int n,int m)//求组合数C(n,m)
{
    if(n<0||m<0||m>n)return 0;
    return fac[n]*invfac[m]%mod*invfac[n-m]%mod;
}
int main()
{
    int t;
    cin>>t;
    init();
    while(t--)
    {
        int n,m,k;
        scanf("%d%d%d",&n,&m,&k);
        ll ans=0;
        for(int c=0;c<=k/n;c++)
        {
            if(c&1)
            {
                ans=(ans-C(m,c)*C(k+m-c*n-1,m-1)%mod+mod)%mod;
            }
            else ans=(ans+C(m,c)*C(k+m-c*n-1,m-1)%mod)%mod;
        }
        printf("%I64d
",ans);
    }
    return 0;
}