hdu 6395 Sequence (分段矩阵快速幂）

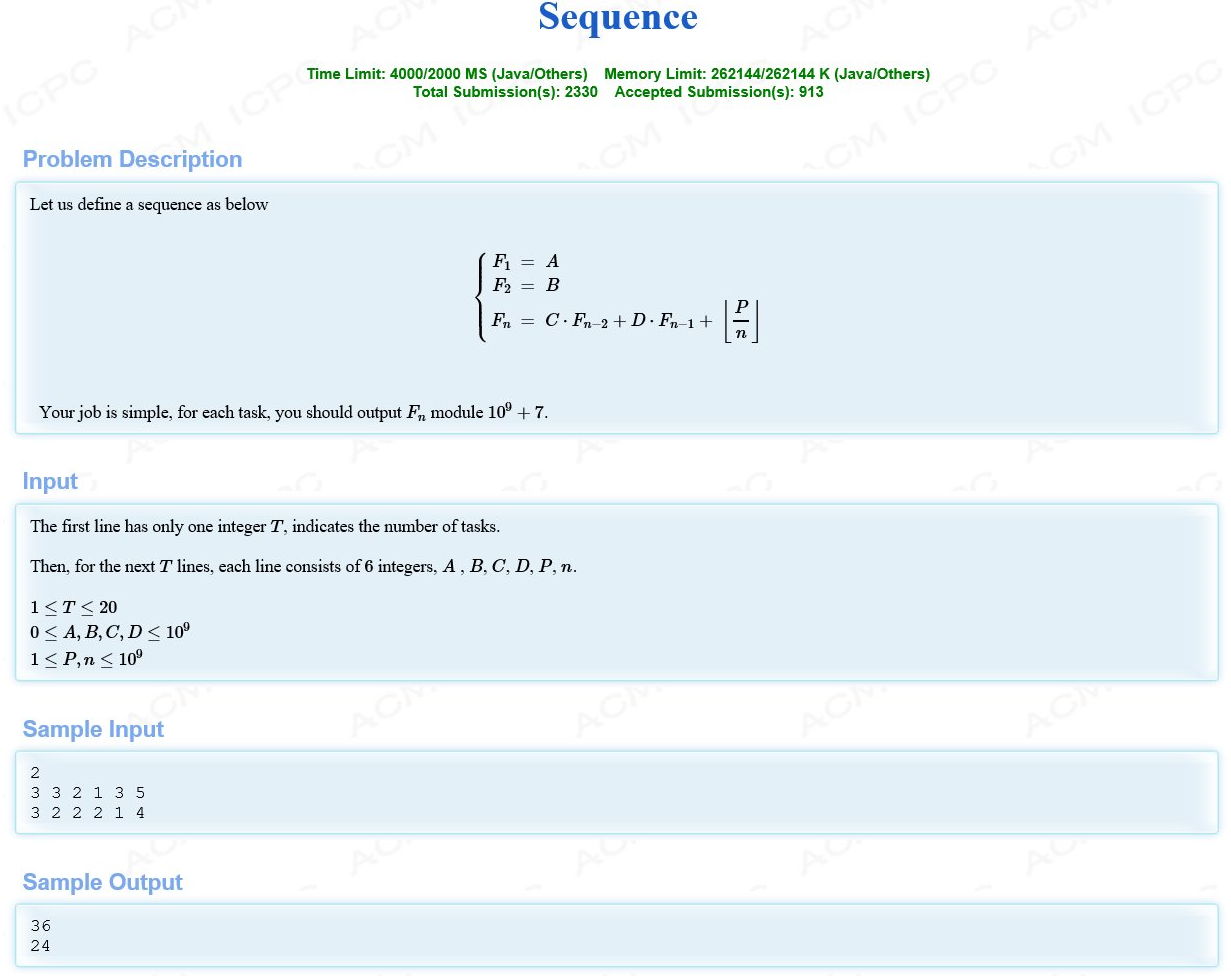
 题意：就是一个矩阵快速幂的题目，难点在于p/n向下取整

解法一：

构造递推式：

这种构造方式很好想，可以发现递推矩阵T与一般矩阵不同之处在于p/n的值一直在变

所以我们不能直接用矩阵快速幂把递推矩阵乘上n-2次

所以此时用到分段的思想：

在某一个区间内，p/i的值是相同的

经过计算这个区间是(i,p/(p/i))

所以我们对每一段用矩阵快速幂即可

从F3一直计算到Fn,一共计算n-2次

值的注意的是n>p时的情况，先计算到Fp,后面p/n都等于0，直接矩阵快速幂到Fn

以及当p==1时，需要特判（因为p-2为负数）

还有要注意矩阵左乘右乘，根据递推式应该是一直右乘，学高代的都知道结果会有很大区别

最后结果为Fn=(ans[0][0]*F2%mod+ans[0][1]*F1%mod+ans[0][2])%mod;

AC代码：

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int mod=1e9+7;
struct mat
{
    LL a[3][3];
};
mat matmul(mat x,mat y)
{
    mat res;
    memset(res.a,0,sizeof res.a);
    int i,j,k;
    for(i=0;i<3;i++)
    {
        for(j=0;j<3;j++)
        {
            for(k=0;k<3;k++)
            {
                res.a[i][j]+=x.a[i][k]*y.a[k][j]%mod;
                res.a[i][j]%=mod;
            }
        }
    }
    return res;
}
mat matpow(mat x,LL n)
{
    mat res;
    memset(res.a,0,sizeof res.a);
    for(int i=0;i<3;i++)res.a[i][i]=1;
    while(n>0)
    {
        if(n&1)res=matmul(res,x);
        x=matmul(x,x);
        n>>=1;
    }
    return res;
}
void solve()
{
    LL a,b,c,d,p,n;
    scanf("%I64d%I64d%I64d%I64d%I64d%I64d",&a,&b,&c,&d,&p,&n);
    mat t,ans;
    memset(t.a,0,sizeof t.a);
    memset(ans.a,0,sizeof ans.a);
    for(int i=0;i<3;i++)ans.a[i][i]=1;
    t.a[0][0]=d;
    t.a[0][1]=c;
    t.a[1][0]=1;
    t.a[2][2]=1;
    if(n==1)printf("%I64d
",a);
    else if(n==2)printf("%I64d
",b);
    else
    {
        LL i,j;
        if(p>=n)
        {
            for(i=3;i<=n;i=j+1)
            {
                j=p/(p/i);
                t.a[0][2]=p/i;
                mat pos=matpow(t,min(j-i+1,n-i+1));
                ans=matmul(pos,ans);
            }
        }
        else
        {
            for(i=3;i<=p;i=j+1)
            {
                j=p/(p/i);
                t.a[0][2]=p/i;
                mat pos=matpow(t,j-i+1);
                ans=matmul(pos,ans);
            }
            t.a[0][2]=0;
            mat pos;
            if(p==1)pos=matpow(t,n-2);
            else pos=matpow(t,n-p);
            ans=matmul(pos,ans);
        }
        LL res=(ans.a[0][0]*b%mod+ans.a[0][1]*a%mod+ans.a[0][2])%mod;
        printf("%I64d
",res);
    }
}
int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        solve();
    }
    return 0;
}

 解法二：

构造递推式https://blog.csdn.net/riba2534/article/details/81672080

这种方法递推矩阵是没有变的

还是要分段去乘

AC代码：

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int mod=1e9+7;
struct mat
{
    LL a[3][3];
};
mat matmul(mat a,mat b)
{
    mat c;
    memset(c.a,0,sizeof c.a);
    int i,j,k;
    for(i=0;i<3;i++)
    {
        for(j=0;j<3;j++)
        {
            for(k=0;k<3;k++)
            {
                c.a[i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j]%mod)%mod;
            }
        }
    }
    return c;
}
mat matpow(mat a,LL b)
{
    mat ans;
    memset(ans.a,0,sizeof ans.a);
    for(int i=0;i<3;i++)ans.a[i][i]=1;
    while(b>0)
    {
        if(b&1)ans=matmul(ans,a);
        a=matmul(a,a);
        b>>=1;
    }
    return ans;
}
void solve()
{
    LL a,b,c,d,p,n;
    scanf("%lld%lld%lld%lld%lld%lld",&a,&b,&c,&d,&p,&n);
    if(n==1)printf("%lld
",a);
    else
    {
        mat t,sta;
        memset(t.a,0,sizeof t.a);
        memset(sta.a,0,sizeof sta.a);
        t.a[0][0]=d;
        t.a[1][0]=c;
        t.a[0][1]=1;
        t.a[2][2]=1;
        t.a[2][0]=1;
        sta.a[0][0]=b;
        sta.a[0][1]=a;
        if(p>=n)
        {
            LL i,j;
            for(i=3;i<=n;i=j+1)
            {
                j=p/(p/i);
                sta.a[0][2]=p/i;
                mat pos=matpow(t,min(j-i+1,n-i+1));
                sta=matmul(sta,pos);
            }
        }
        else
        {
            LL i,j;
            for(i=3;i<=p;i=j+1)
            {
                j=p/(p/i);
                sta.a[0][2]=p/i;
                mat pos=matpow(t,j-i+1);
                sta=matmul(sta,pos);
            }
            sta.a[0][2]=0;
            mat pos;
            if(p<3)pos=matpow(t,n-2);
            else pos=matpow(t,n-p);
            sta=matmul(sta,pos);
        }
        printf("%lld
",sta.a[0][0]);
    }
}
int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        solve();
    }
    return 0;
}