A:
每个学生所得的bamboo的score的值必须大于或等于他的幸运数字, bamboo的score值就是其长度x的欧拉函数值(即小于x且与x互质的数的个数)
每单位长度花费1Xukha,求买这些bamboo的最小花费。
此题关键:素数(x)的欧拉函数值(x-1)是满足条件(大于等于幸运数字)且花费最小的,相同欧拉函数值合数数值(花费)一定更大,所以只要筛出【1,1e6】的素数即可。
B:
二分图匹配
C:
给你面积为a的地毯并告诉你地毯的最小边长b,求出有多少种不同的地毯。
用到算术基本定理(唯一分解定理)

用第一条计算出a所有正因子的个数,除以2即得a正因子的对数,然后暴力枚举筛掉(1,b)以内的正因子对数
D:
r(n)=n的全体正因数之和
给你一个n(n<=1e12),求出(1,n)内所有正因数和为偶数的数的个数
由公式可以推知,若要r(n)为奇数,
则每一个质因子的括号都要为奇数,除了2是偶数以外,其他素数都是奇数
于是抛开质因子2不谈,n都要包含其他的质因子的偶数个
即n是一个完全平方数,或者是完全平方数的两倍,于是用n-sqrt(n)-sqrt(n/2)即得到答案
E:
求n^k的前三位和后三位。
后三位很好求,用n^k(mod 1000)即可,避免溢出要用快速幂取模1000
前三位
假设n^k=10^a=10^(x+y),x是a的整数部分,y是小数部分,那么显然10^x用于控制n^k的位数,10^y才代表n^k的值
而由于0<y<1,10^0=1 < 10^y < 10^1=10
故前三位等于10^y*100
使用fmod(a, 1)表示求浮点型数 a 的小数部分。
int strat=(int)pow(10.0,2.0+fmod(k*log10(n*1.0),1.0));
求2^n,直接1<<n;
顺便记录一下刚做的CF某D题,为了不T,用到双向队列,把对x,y消耗少的总是放到队首,下次取点的时候总是先考虑这些点。
std::deque<Node> q; q.push_back((Node) {r, c, X, Y});
if(i == 0 || i == 1) {q.push_front((Node) {wx, wy, p.l, p.r}); continue;}
if(i == 2) {q.push_back((Node) {wx, wy, p.l - 1, p.r}); continue;}
F:
欧拉筛素数筛到1e7即可。
G:
求和n/1+n/2+n/3+......+n/n。
直接算会T
发现y=n/x关于y=x的对称点是sqrt(n)
所以直接求(1,sqrt(n))的和再乘以2,再减去重复的sqrt(n)*sqrt(n)即可
H:
求有多少对(a,b) (a<=b)使得 lcm(a,b)=n。
算术基本定理:求约数,倍数,质因子个数及和。
一个数的每一个质因子的不同幂对应不同的因子。
假设lcm(a,b)=n,那么a,b必然是n的因子:

I:
求调和级数 1/1+1/2+1/3+......+1/n。(n<=1e8)

//打表 #include <iostream> #include <cstdio> #define N 100000000 using namespace std; double a[N /100 + 5]; void init() { a[0] = 0; a[1] = 1; double t = 1.0; for (int i = 2; i <= N; i++) { t = t + 1.0 / i; if (i % 100 == 0) { a[i /100] = t; } } } int main() { init(); int T; scanf("%d", &T); for (int cas = 1; cas <= T; cas++) { int n; scanf("%d", &n); int t = n / 100; double sum = a[t]; for (int i = t * 100 + 1; i <= n; i++) { sum += 1.0 / i; } printf("Case %d: %.10lf ", cas, sum); } return 0; }
J:
给你一个整数n(可能为负数),让你求满足a^p=n的最大的p。
我的抖机灵(不知正确否)用到C++库函数 log() 及换底公式
log(a,b)(以a为底b的对数)=log(b) / log(a) ,直接找出最大的p。
正确解答:
思路:当n是正数时,直接对n进行素因子分解,在对它的素因子的个数进行gcd,比如12=2^2*3,gcd(2,1)就是最大的p;
当n是负数时,则p的值一定是奇数,因为一个数的偶数次方一定为整数,因此需要将它的素因子个数全都化为奇数后再求gcd。
CF 1059.C
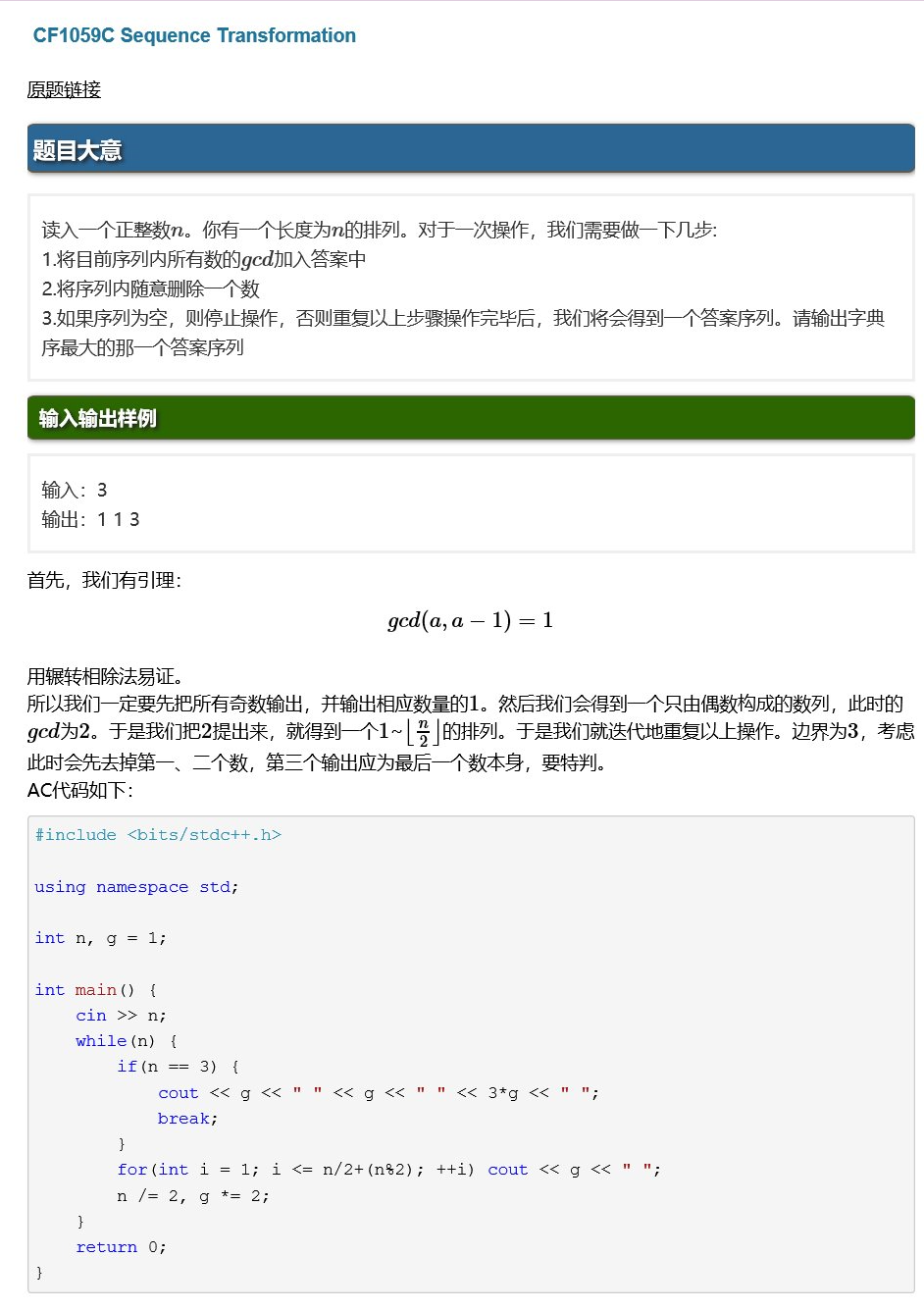
K:判断a是否整除b,10^(-200)<=a<=10^200.b<=1e9.
直接上JAVA大数把。
L:
推公式的题目,推出结果为 k*n^(k-1)*(A[0]+A[1]+A[2]+......+A[n-1]) 。
M:求(a,b)内素数的个数,a,b<=1e9,b-a<=100000.
区间素数筛,先预处理1到sqrt(b)即1e5以内的素数,然后用这些素数的倍数(大于等于2倍)筛掉[a,b]区间的合数。最后遍历结果数组统计素数个数,因为a,b范围较大,离散化一下数组下标变成0到b-a。(从a偏移到0)特判a=1的情况,1用素数筛不掉。