uva 1045 最佳完美匹配 km算法 && 枚举

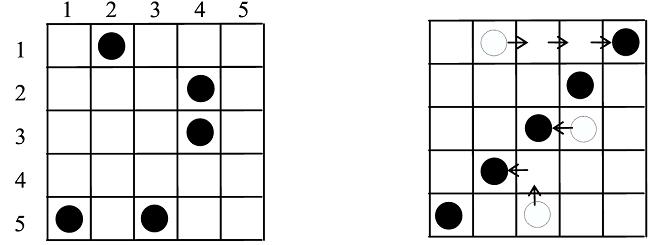
Hua and Shen have invented a simple solitaire board game that they call ``The Great Wall Game." The game is played with n stones on an n×n grid. The stones are placed at random in the squares of the grid, at most one stone per square. In a single move, any single stone can move into an unoccupied location one unit horizontally or vertically in the grid. The goal of the puzzle is to create a ``wall," i.e., to line up all n stones in a straight line either horizontally, vertically, or diagonally using the fewest number of moves. An example for the case n = 5 is shown in Figure 1(a). In Figure 1(b) it is shown that with six moves we can line all the stones up diagonally. No smaller number of moves suffices to create a line of five stones. (However, there are other solutions using six moves, e.g., we can line up all five stones in the third column using six moves.)

Figure 1. Starting board (a) and a 6-move solution (b) for n = 5

There is just one problem - Hua and Shen have no idea what the minimum number of moves is for any given starting board. They would like you to write a program that can take any starting configuration and determine the fewest number of moves needed to create a wall.

Input 

The input consists of multiple cases. Each case begins with a line containing an integer n, 1n15. The next line contains the row and column numbers of the first stone, followed by the row and column numbers of the second stone, and so on. Rows and columns are numbered as in the above diagram. The input data for the last case will be followed by a line containing a single zero.

Output 

For each input case, display the case number (1, 2,...) followed by the minimum number of moves needed to line up the n stones into a straight-line wall. Follow the format shown in the sample output. Print a blank line after each case.

Sample Input 

5                                                                
1 2 2 4 3 4 5 1 5 3                                             
2                                                                
1 1 1 2                                                         
3                                                                
3 1 1 2 2 2                                                       
0

Sample Output 

Board 1: 6 moves required.
  
Board 2: 0 moves required.
  
Board 3: 1 moves required.

参考：http://blog.csdn.net/jayye1994/article/details/10050695

总共有2*n+2种情况，枚举即可。
为什么对某个石头它一定可以走最短路到当前枚举点？ ---。。。
（PS，YY资源短缺啊，都是看别人分析，自己苦力代码）
AC代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<vector>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<map>

using namespace std;

#define LL long long
#define ULL unsigned long long
#define UINT unsigned int
#define MAX_INT 0x7fffffff
#define cint const int
#define MAX(X,Y) ((X) > (Y) ? (X) : (Y))
#define MIN(X,Y) ((X) < (Y) ? (X) : (Y))
#define INF 100000000
#define MAXN 20
#define MAXM 880

int x[MAXN], y[MAXN];
bool s[MAXN], t[MAXN];
int lft[MAXN], n, w[MAXN][MAXN], slack[MAXN];

int lx[MAXN], ly[MAXN];

bool match(int u){
    s[u]=true;
    for(int v=1; v<=n; v++){
        if(t[v]) continue;
        int d=lx[u]+ly[v]-w[u][v];
        if(!d){
            t[v]=true;
            if(lft[v]==-1 || match(lft[v])){
                lft[v]=u;
                return true;
            }
        }
        else slack[v]=MIN(slack[v], d);
    }
    return false;
}

int km(){
    int i, j;
    fill(lft+1, lft+1+n, -1);
    fill(ly+1, ly+1+n, 0);
    for(i=1; i<=n; i++)
        for(j=1, lx[i]=-INF; j<=n; j++)
            lx[i]=MAX(lx[i], w[i][j]);
    for(i=1; i<=n; i++){
        fill(slack+1, slack+1+n, INF);
        while(true){
            fill(s+1, s+1+n, 0);
            fill(t+1, t+1+n, 0);
            if(match(i)) break;
            int d=INF;
            for(j=1; j<=n; j++) if(!t[j])
                d=MIN(d, slack[j]);
            for(j=1; j<=n; j++){
                if(s[j]) lx[j]-=d;
                if(t[j]) ly[j]+=d;
//                else slack[j]-=d;
            }
        }
    }

    int ans=0;
    for(i=1; i<=n; i++)
        ans+=w[lft[i]][i];
    return ans;
}

int solve(){
    int i, j, k, ans=-INF;                  //第k个stone到第i行第j列
    for(i=1; i<=n; i++){
        for(k=1; k<=n; k++)
            for(j=1; j<=n; j++)
                w[k][j]=-abs(x[k]-i)-abs(y[k]-j);
        ans=max(ans, km());
    }
    for(j=1; j<=n; j++){
        for(k=1; k<=n; k++)
            for(i=1; i<=n; i++)
                w[k][i]=-abs(x[k]-i)-abs(y[k]-j);
        ans=max(ans, km());
    }
    for(k=1; k<=n; k++){
        for(i=1; i<=n; i++)
            w[k][i]=-abs(x[k]-i)-abs(y[k]-i);
    }
    ans=max(ans, km());
    for(k=1; k<=n; k++){
        for(i=1; i<=n; i++)
            w[k][i]=-abs(x[k]-i)-abs(y[k]-(n+1-i));
    }
    ans=max(ans, km());
    return -ans;
}

int main(){
//    freopen("C:\Users\Administrator\Desktop\in.txt","r",stdin);
    int kase=1;
    while(scanf(" %d", &n)==1 && n){
        for(int i=1; i<=n; i++)
            scanf(" %d %d", x+i, y+i);
        printf("Board %d: %d moves required.

", kase++, solve());
    }
    return 0;
}