poj 1631 / nlogn 算法 求 最长上升子序列长度

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　Bridging signals

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 10212		Accepted: 5589

Description

'Oh no, they've done it again', cries the chief designer at the Waferland chip factory. Once more the routing designers have screwed up completely, making the signals on the chip connecting the ports of two functional blocks cross each other all over the place. At this late stage of the process, it is too expensive to redo the routing. Instead, the engineers have to bridge the signals, using the third dimension, so that no two signals cross. However, bridging is a complicated operation, and thus it is desirable to bridge as few signals as possible. The call for a computer program that finds the maximum number of signals which may be connected on the silicon surface without crossing each other, is imminent. Bearing in mind that there may be thousands of signal ports at the boundary of a functional block, the problem asks quite a lot of the programmer. Are you up to the task?

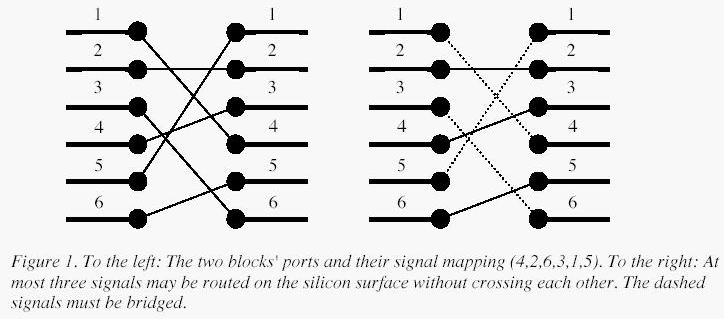
A typical situation is schematically depicted in figure 1. The ports of the two functional blocks are numbered from 1 to p, from top to bottom. The signal mapping is described by a permutation of the numbers 1 to p in the form of a list of p unique numbers in the range 1 to p, in which the i:th number specifies which port on the right side should be connected to the i:th port on the left side.Two signals cross if and only if the straight lines connecting the two ports of each pair do.

Input

On the first line of the input, there is a single positive integer n, telling the number of test scenarios to follow. Each test scenario begins with a line containing a single positive integer p < 40000, the number of ports on the two functional blocks. Then follow p lines, describing the signal mapping:On the i:th line is the port number of the block on the right side which should be connected to the i:th port of the block on the left side.

Output

For each test scenario, output one line containing the maximum number of signals which may be routed on the silicon surface without crossing each other.

Sample Input

4
6
4
2
6
3
1
5
10
2
3
4
5
6
7
8
9
10
1
8
8
7
6
5
4
3
2
1
9
5
8
9
2
3
1
7
4
6

Sample Output

3
9
1
4

Source

Northwestern Europe 2003

 

为什么最多不相交线路对数 == 最长上升子序列长度 ?

1. 若两对线路(l1, r1)/(l2, r2)不交且l1<l2，假设r2<r1，则显然两对线路相较了，所以r2>r1。由此归纳，每增加一对不与《已经不相交port》不相交的Port，形成的序列仍保持上升性质。

 

2.若序列为上升序列，则对应的Port对不相交：视Port对(li, ri)为f(li)=ri的映射(函数)，同1可反证f(li)为递增映射。

 

AC代码：（写了N久，脑子TM秀逗了）

#include<iostream>
#include<cstdio>

using namespace std;

#define MAXN 44444
int a[MAXN], ans[MAXN];

//找到位置i，使ans[i]为最小的≥e的数，用e替换之
void tryToInsert(int &size, int e){
    int l=0, r=size, mid=size>>1;
    while(l<r){
       if(ans[mid] == e) break;
       else if(ans[mid] < e) l = mid + 1;
       else{
            if(r - l < 3){ mid = ans[l] >= e ? l : mid;  break;}
            r = mid + 1;
       }
       mid = (l + r) >> 1;
    }
    ans[mid]=e;
    if(size == mid) size++;
}

//nlogn 解 最长上升子序列
int solve(int n){
    int ansl = 0;    //假定最长上升子序列长度为0
    for(int i=0; i<n; i++)
        tryToInsert(ansl, a[i]);
    return ansl;
}

int main(){
    int t, n;
    scanf(" %d", &t);
    while(t--){
        scanf(" %d", &n);
        for(int i=0; i<n; i++) scanf(" %d", a+i);
        printf("%d
", solve(n));
    }
    return 0;
}