13.随机变量的分布
离散型的很简单 因为都是可列的值 所以我们重点考虑连续型

连续型:

就是我们根据x和y的关系 把Y=g(X)带进去求Y的概率密度 并且我们要注意一些细节(比如和y的定义域我们要求交集)、
但是这只是纯理论 掌握这里的知识要用例题
第二种方法是公式法:

例题(第一种方法):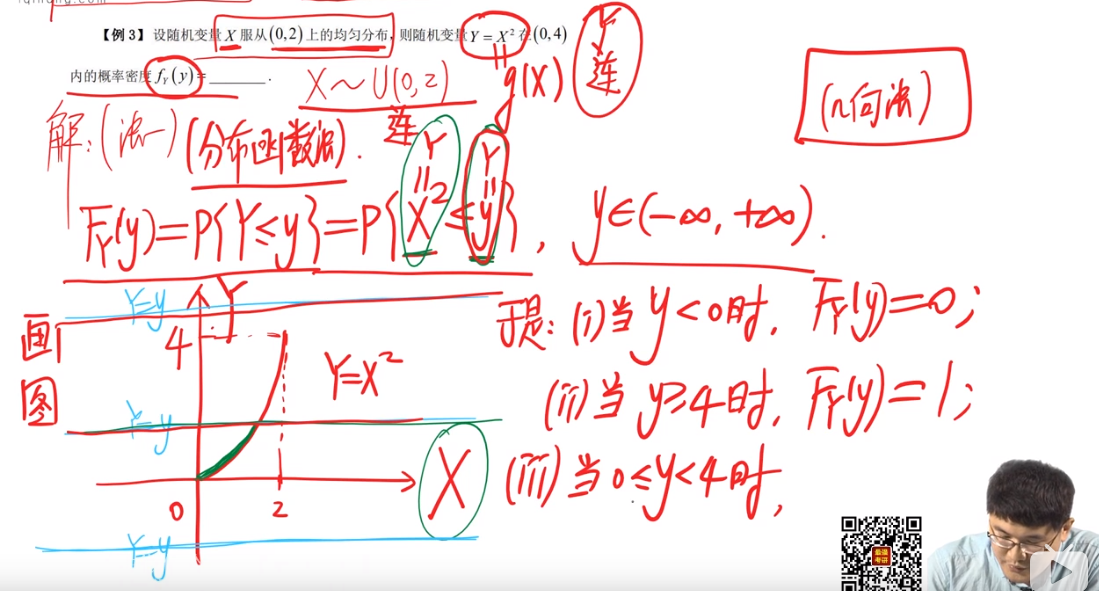
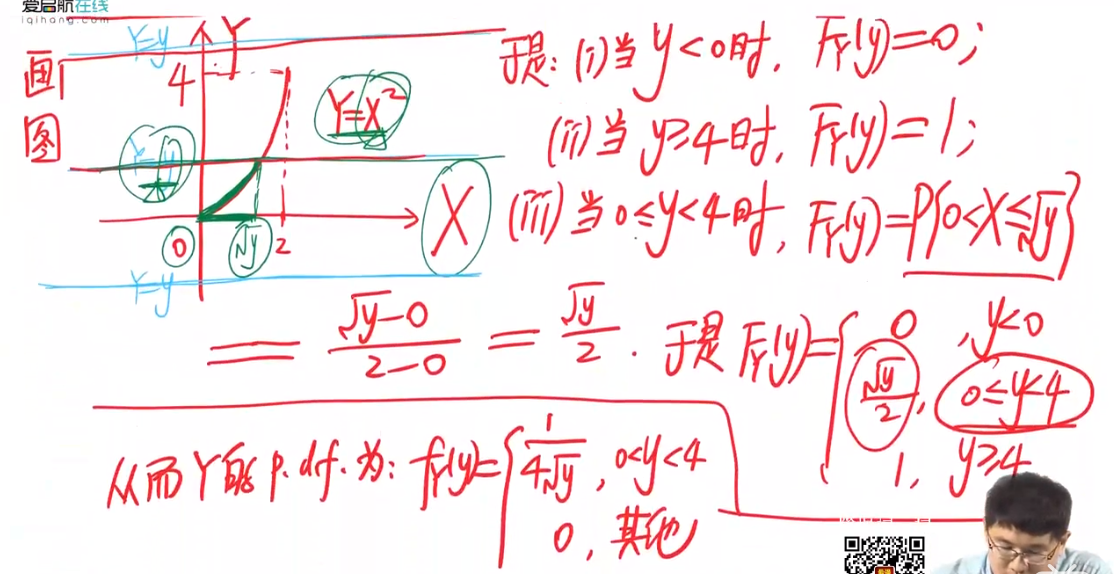
今后复习应该着重这种类型题 因为需要大量练习
公式法:

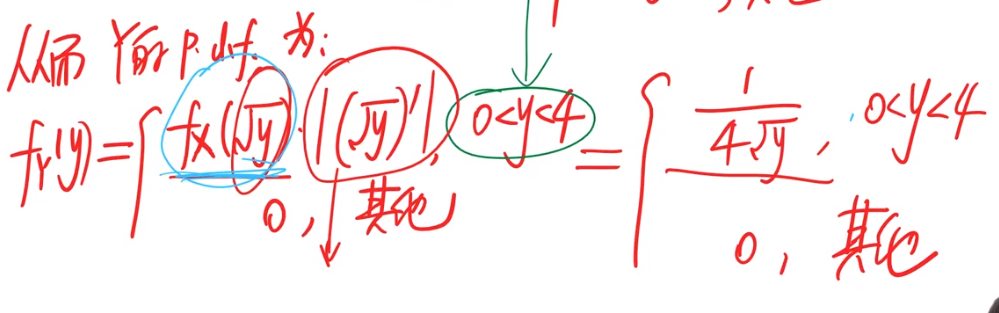
之后就是复习 多维随机变量这个模块了 这个也是比较重要的
14. 多维随机变量及其分布


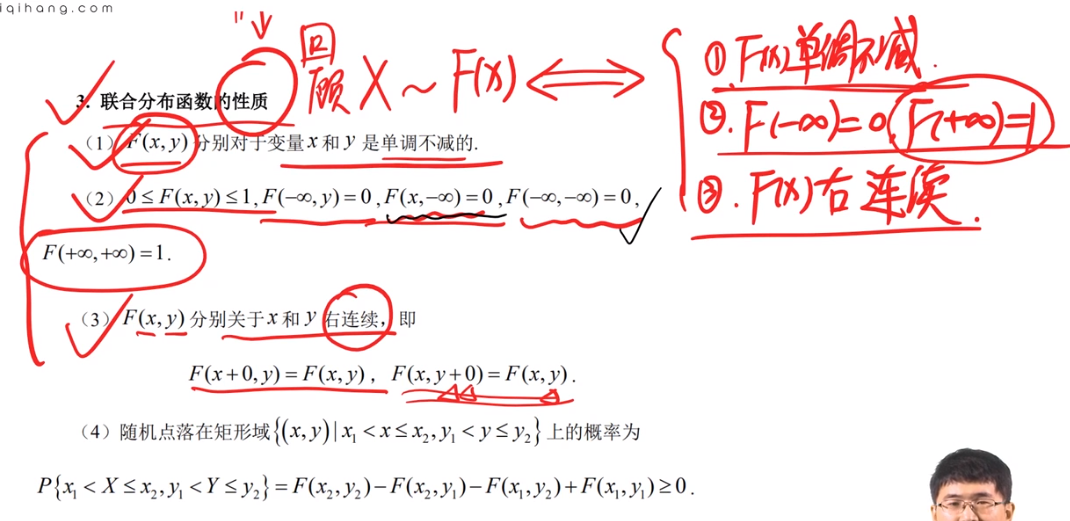
15.二维离散型随机变量的概率分布 边缘分布 条件分布

剩下的边缘分布条件分布略
16.二维连续型随机变量的概率密度 边缘密度 条件密度



条件= 联合/边缘
17.随机变量的独立性

也就是联合= 边缘*边缘
性质:

18. 常见二维随机变量的分布

大纲只要求这两种
均匀分布:

正态分布的性质:

对于一般的随机变量 独立推出不相关 但是对于二维正态 不相关也能推出独立
19..二维随机变量的分布
离散型随机变量的分布

这种混合型的 看题吧:

有限可加性:

但是 我们用全概率公式 也能有这种结果
殊途同归

还有一种情形 两个都是连续的:(近几年没考过)

对于都是连续的:
方法:



推广的卷积公式记忆有点烦 所以要学会现推

例题:好懂

毕竟啊均匀分布

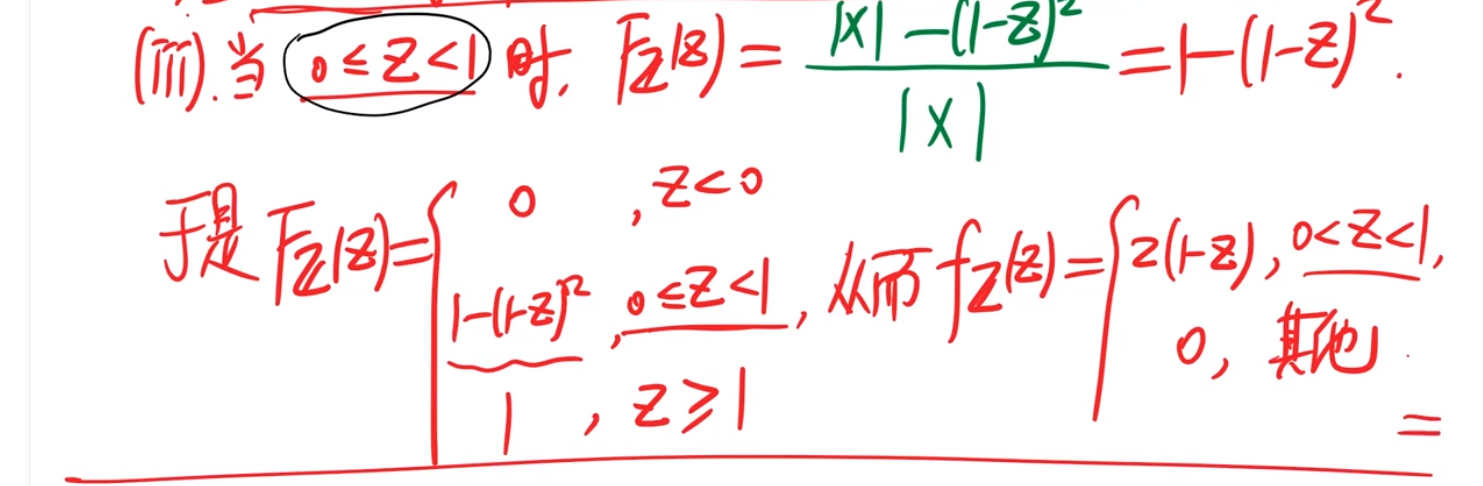
两个连续型是难点啊 得多练习
卷积的两个思路:
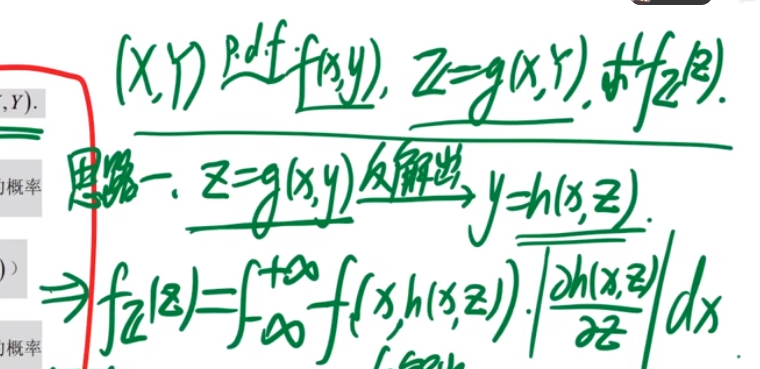
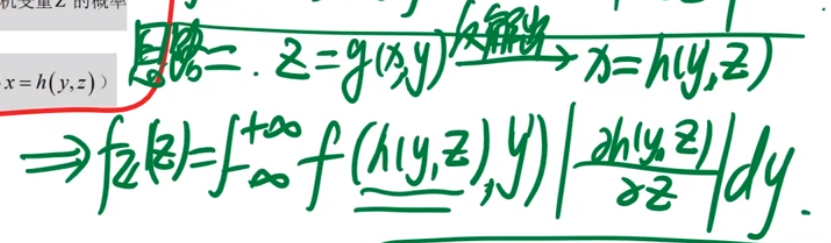
接着看最值:
