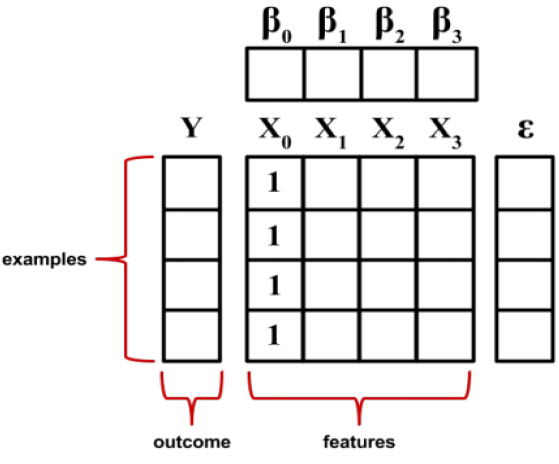
线性回归
•如何使用R准备数据进行回归分析
•定义一个线性方程并估计回归模型
理解回归
•“回归平均值”(regression to the mean)
•回归问题主要关注确定一个唯一的因变量(dependent variable)(需要预测的值)和一个或多个数值型的自变量(independent variables)(预测变量)之间的关系
•广义线性回归,GLM。比如,逻辑回归,泊松回归。
•对于简单线性回归问题,也就是小学大家就都会了的解应用题。Y=a+bx
•线性回归,是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。其表达形式为y = w'x+e,e为误差服从均值为0的正态分布。
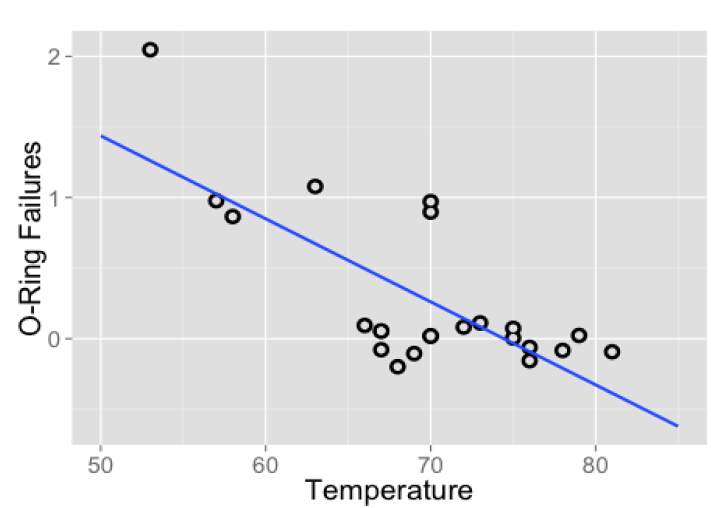
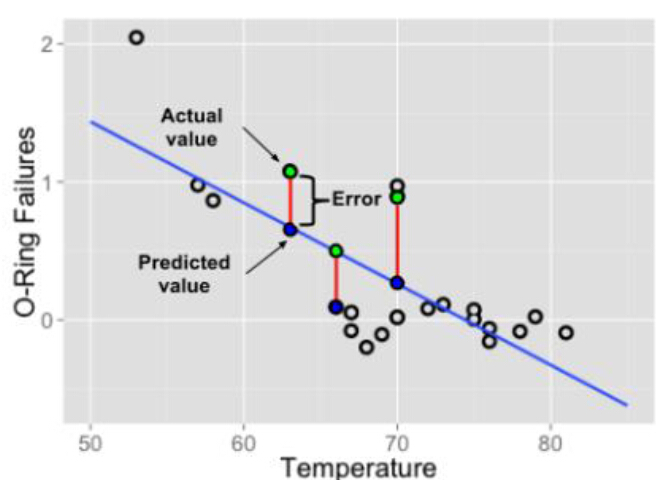
最小二乘法
•最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
•一般来说,线性回归都可以通过最小二乘法求出其方程,可以计算出对于y=bx+a的直线
相关系数
•两个变量之间的相关系数是一个数,它表示两个变量服从一条直线的关系有多麽紧密
•相关系数就是指Pearson相关系数,它是数学家Pearson提出来的,相关系数的范围是-1~+1之间,两端的值表示一个完美的线性关系
•相关系数接近于0则表示不存在线性关系。协方差函数cov(),标准方差函数sd(),可以求出来cor()
多元线性回归
•在回归分析中,如果有两个或两个以上的自变量,就称为多元回归。事实上,一种现象常常是与多个因素相联系的,由多个自变量的最优组合共同来预测或估计因变量,比只用一个自变量进行预测或估计更有效,更符合实际。因此多元线性回归比一元线性回归的实用意义更大。
•大多数现实世界的分析不止一个自变量,大多数情况下,很有可能使用多元线性回归