并查集用来处理集合之间的关系,动态地维护和处理集合元素之间复杂的关机,快速合并,反复查找某元素所在的集合。
用一种通俗的说法就是1号和2号是亲戚,2号和3号是亲戚,则1号和3号是亲戚

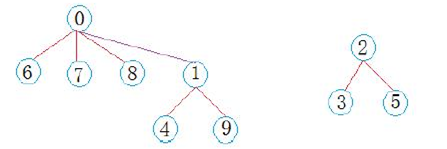
类似于上图
**************************************
根据书上所述
应该有两种方法

不要在意上面的字啦。。。。。。。。。。。。
最最最上面的图方法会超时
下面这幅就高大上了,人家不会超时
上面是串成糖葫芦式,下面名曰路径压缩。。其实就是所有子子孙孙都黏在他们祖先上
**********************************************
例题
• 【例4-9】、亲戚(relation)
• 【问题描述】
• 或许你并不知道,你的某个朋友是你的亲戚。他可能是你的曾祖父的外公的女婿的外甥女的表姐的孙子。如果能得到完整的家谱,判断两个人是否亲戚应该是可行的,但如果两个人的最近公共祖先与他们相隔好几代,使得家谱十分庞大,那么检验亲戚关系实非人力所能及。在这种情况下,最好的帮手就是计算机。为了将问题简化,你将得到一些亲戚关系的信息,如Marry和Tom是亲戚,Tom和Ben是亲戚,等等。从这些信息中,你可以推出Marry和Ben是亲戚。请写一个程序,对于我们的关于亲戚关系的提问,以最快的速度给出答案。
• 【输入格式】
• 输入由两部分组成。
• 第一部分以N,M开始。N为问题涉及的人的个数(1≤N≤20000)。这些人的编号为1,2,3,…, N。下面有M行(1≤M≤1 000 000),每行有两个数ai, bi,表示已知ai和bi是亲戚。
• 第二部分以Q开始。以下Q行有Q个询问(1≤Q≤1 000 000),每行为ci, di,表示询问ci和di是否为亲戚。
• 【输出格式】
• 对于每个询问ci, di,输出一行:若ci和di为亲戚,则输出“Yes”,否则输出“No”。
• 【输入样例】
• 10 7
• 2 4
• 5 7
• 1 3
• 8 9
• 1 2
• 5 6
• 2 3
• 3
• 3 4
• 7 10
• 8 9
• 【输出样例】
• Yes
• No
• Yes
***********************************
超时的那种
1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 #define maxn 20001 5 int father[maxn]; 6 int m,n,i,x,y,q; 7 /* 8 int find(int x) //用非递归的实现 9 { 10 while (father[x] != x) x = father[x]; 11 return x; 12 } 13 */ 14 int find(int x) //用递归的实现 15 { 16 if (father[x] != x) return find(father[x]); 17 else return x; 18 } 19 void unionn(int r1,int r2) 20 { 21 father[r2] = r1; 22 } 23 int main() 24 { 25 freopen("relation.in","r",stdin); 26 freopen("relation.out","w",stdout); 27 cin >> n >> m; 28 for (i = 1; i <= n; i++) 29 father[i] = i; //建立新的集合,其仅有的成员是i 30 for (i = 1; i <= m; i++) 31 { 32 scanf("%d%d",&x,&y); 33 int r1 = find(x); 34 int r2 = find(y); 35 if (r1 != r2) unionn(r1,r2); 36 } 37 cin >> q; 38 for (i = 1; i <= q; i++) 39 { 40 scanf("%d%d",&x,&y); 41 if (find(x) == find(y)) printf("Yes "); 42 else printf("No "); 43 } 44 return 0; 45 }
**************************************************************
路径压缩就可以减少时间复杂度
1 #include<cstdio> 2 #include<algorithm> 3 #include<cmath> 4 #include<cstring> 5 using namespace std; 6 #define maxn 20001 7 int father[maxn]; 8 int m,n,i,x,y,q; 9 int find(int x) 10 { 11 if(father[x] != x) 12 father[x] = find(father[x]); 13 return father[x]; 14 } //递归 15 void unionm(int x,int y) 16 { 17 x = find(x); 18 y = find(y); 19 father[y] = x; 20 } //指向祖先 21 int main() 22 { 23 cin >> n >> m; 24 for(int i = 1;i <= n;i++) 25 { 26 father[i] = i; 27 } 28 for(int i = 1;i <= m;i++) 29 { 30 scanf("%d %d",&x,&y); 31 int r1 = find(x); 32 int r2 = find(y); 33 if(r1 != r2) 34 { 35 unionm(r1,r2); 36 } 37 cin >> q; 38 for(int i = 1;i <= q,i++) 39 { 40 scanf("%d %d",&x,&y); 41 if(find(x) == find(y)) 42 printf("Yes "); 43 else 44 printf("No "); 45 46 } //比较 47 return 0; 48 } 49 }
**********************************
odk第一篇博客热乎乎的出炉啦**************
撒花✿✿ヽ(°▽°)ノ✿