递归与尾递归
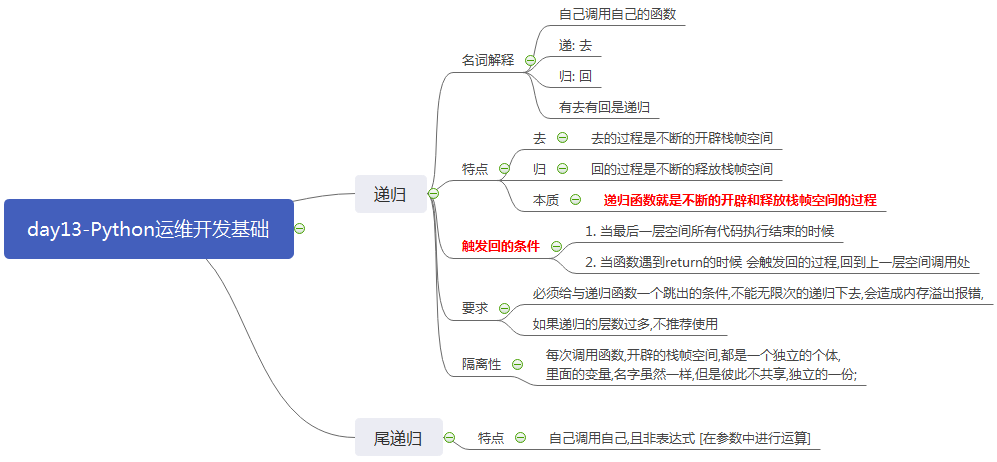

# ### 递归函数 """ 递归函数: 自己调用自己的函数 递:去 归:回 有去有回是递归 """ # 简单递归 def digui(n): print(n,"<===1===>") if n > 0: digui(n-1) print(n,"<===2===>") digui(5) """ # 代码解析: 去的过程 n = 5 print(5,"<===1===>") 5>0 满足 digui(n-1) -> digui(5-1) -> digui(4) 代码在13行,暂定阻塞 n = 4 print(4,"<===1===>") 4>0 满足 digui(n-1) -> digui(4-1) -> digui(3) 代码在13行,暂定阻塞 n = 3 print(3,"<===1===>") 3>0 满足 digui(n-1) -> digui(3-1) -> digui(2) 代码在13行,暂定阻塞 n = 2 print(2,"<===1===>") 2>0 满足 digui(n-1) -> digui(2-1) -> digui(1) 代码在13行,暂定阻塞 n = 1 print(1,"<===1===>") 1>0 满足 digui(n-1) -> digui(1-1) -> digui(0) 代码在13行,暂定阻塞 n = 0 print(0,"<===1===>") 0>0 不满足 print(0,"<===2===>") 回的过程 n = 1 从上一次13行的位置,往下执行, print(1,"<===2===>") n = 2 从上一次13行的位置,往下执行, print(2,"<===2===>") n = 3 从上一次13行的位置,往下执行, print(3,"<===2===>") n = 4 从上一次13行的位置,往下执行, print(4,"<===2===>") n = 5 从上一次13行的位置,往下执行, print(5,"<===2===>") """ """ 每调用一次函数就会开辟栈帧空间 n = 5 n = 4 n = 3 n = 2 n = 1 n = 0 n = 1 n = 2 n = 3 n = 4 n = 5 """ """ # 总结: 递归函数特点1: 有去有回是递归,去的过程是不断的开辟栈帧空间,回的过程是不断的释放栈帧空间,递归函数就是不断的开辟和释放栈帧空间的过程 递归函数特点2: 递归函数触发回的过程一共有2点:(1) 当最后一层空间所有代码执行结束的时候 (2)当函数遇到return的时候 会触发回的过程,回到上一层空间调用处 递归函数特点3: 必须给与递归函数一个跳出的条件,不能无限次的递归下去,会造成内存溢出报错,如果递归的层数过多,不推荐使用 递归函数特点4: 每次调用函数,开辟的栈帧空间,都是一个独立的个体,里面的变量,名字虽然一样,但是彼此不共享,独立的一份; """ # 默认递归深度是1000层 , 当前电脑是995层 """ def deep(): deep() deep() """

# 求5的阶乘 5! = 5*4*3*2*1 n = 5 total = 1 for i in range(5,0,-1): total *= i # total = total * i => 1 * 5 # total = total * i => 1 * 5 * 4 # total = total * i => 1 * 5 * 4 * 3 # total = total * i => 1 * 5 * 4 * 3 * 2 # total = total * i => 1 * 5 * 4 * 3 * 2 * 1 print(total) def jiecheng(n): if n <= 1: return 1 return n * jiecheng(n-1) res = jiecheng(5) print(res) """ # 代码解析: 去的过程 n = 5 return n * jiecheng(n-1) => 5 * jiecheng(4) n = 4 return n * jiecheng(n-1) => 4 * jiecheng(3) n = 3 return n * jiecheng(n-1) => 3 * jiecheng(2) n = 2 return n * jiecheng(n-1) => 2 * jiecheng(1) n = 1 return 1 回的过程 n = 2 return n * jiecheng(n-1) => 2 * 1 n = 3 return n * jiecheng(n-1) => 3 * 2 * 1 n = 4 return n * jiecheng(n-1) => 4 * 3 * 2 * 1 n = 5 return n * jiecheng(n-1) => 5 * 4 * 3 * 2 * 1 return 120 """ # 尾递归: 自己调用自己,且非表达式 [在参数中进行运算] """ 可以简化逻辑:只需要考虑去的过程,不需要考虑回的过程,减少逻辑(推荐) 去的过程,最后一层空间的返回值,就是回的过程,最上层空间所能够接受到的值 理论上,尾递归只开辟一个栈帧空间,但cpython解释器不支持,大型的服务厂商有自己独立的解释器可以支持; """ def jiecheng(n,endval): if n <= 1: return endval return jiecheng(n-1,n*endval) res = jiecheng(5,1) print(res) """ # 代码解析: 去的过程 n=5,endval=1 return jiecheng(n-1,n*endval) => jiecheng(5-1,5*1) => jiecheng(4,5*1) n=4,endval=5*1 return jiecheng(n-1,n*endval) => jiecheng(4-1,5*1*4) => jiecheng(3,5*1*4) n=3,endval=5*1*4 return jiecheng(n-1,n*endval) => jiecheng(3-1,5*1*4*3) => jiecheng(2,5*1*4*3) n=2,endval=5*1*4*3 return jiecheng(n-1,n*endval) => jiecheng(2-1,5*1*4*3*2) => jiecheng(1,5*1*4*3*2) n=1,n <= 1 , return endval 回的过程 n=2 return 5*1*4*3*2 n=3 return 5*1*4*3*2 n=4 return 5*1*4*3*2 n=5 return 5*1*4*3*2 """ # 斐波那契数列: 1,1,2,3,5,8,13,21,34,55 ,.... 第n个数字是几? def feib(n): if n == 1 or n == 2: return 1 return feib(n-1)+feib(n-2) res = feib(5) print(res) """ # 代码解析: n = 5 return feib(4) + feib(3) feib(4) [=>3] + feib(3) [2] feib(3) + feib(2) feib(2) + feib(1) feib(2) + feib(1) + 1 1 + 1 1 + 1 """
day13
