题目描述
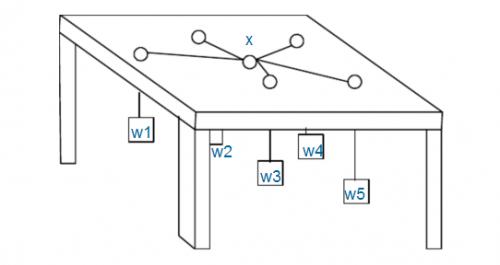
如图:有n个重物,每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞,然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的(不会造成能量损失),桌子足够高(因而重物不会垂到地上),且忽略所有的摩擦。
问绳结X最终平衡于何处。
注意:桌面上的洞都比绳结X小得多,所以即使某个重物特别重,绳结X也不可能穿过桌面上的洞掉下来,最多是卡在某个洞口处。
输入输出格式
输入格式:
文件的第一行为一个正整数n(1≤n≤1000),表示重物和洞的数目。接下来的n行,每行是3个整数:Xi.Yi.Wi,分别表示第i个洞的坐标以及第 i个重物的重量。(-10000≤x,y≤10000, 0<w≤1000 )
输出格式:
你的程序必须输出两个浮点数(保留小数点后三位),分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。
输入输出样例
输入样例#1:
3
0 0 1
0 2 1
1 1 1
输出样例#1:
0.577 1.000
说明
[JSOI]
题解
- 早就想打一道模拟退火的题,但由于种种原因迟迟没有打
- 今天由于
机缘巧合巨佬讲题,有幸A掉这道模拟退火的模板题 -
先来了解一下物理上的退火
-
模拟退火的出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法是一种通用的优化算法,其物理退火过程由加温过程、等温过程、冷却过程这三部分组成。
-
原理
-
模拟退火的原理也和金属退火的原理近似:将热力学的理论套用到统计学上,将搜寻空间内每一点想像成空气内的分子;分子的能量,就是它本身的动能;而搜寻空间内的每一点,也像空气分子一样带有“能量”,以表示该点对命题的合适程度。演算法先以搜寻空间内一个任意点作起始:每一步先选择一个“邻居”,然后再计算从现有位置到达“邻居”的概率。
- 其实这些都是废话,在OI中要注意的其实只有三点
模拟退火算法的应用很广泛,可以求解NP完全问题
(1) 温度T的初始值设置问题
温度T的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一、初始温度高,则搜索到全局最优解的可能性大,但因此要花费大量的计算时间; 反之,则可节约计算时间,但全局搜索性能可能受到影响。实际应用过程中,初始温度一般需要依据实验结果进行若干次调整。
(2) 退火速度问题。
模拟退火算法的全局搜索性能也与退火速度密切相关。一般来说,同一温度下的“充分”搜索(退火)是相当必要的,但这需要计算时间。实际应用中,要针对具体问题的性质和特征设置合理的退火平衡条件。
(3) 温度管理问题。
温度管理问题也是模拟退火算法难以处理的问题之一。实际应用中,由于必须考虑计算复杂度的切实可行性等问题,常采用如下所示的降温方式:
式中k为正的略小于1.00的常数,t为降温的次数。
- 总的来说就是模拟退火算法就是需要我们以一定几率接受次优解,从而跳出局部最优达到整体最优的算法,但因为是随机,所以我们可以多跑几遍,在时间允许的范围内尽量找到正解
Code
#include<bits/stdc++.h>
#define in(i) (i=read())
using namespace std;
const double delta=0.9969;//降温系数
int read() {
int ans=0,f=1; char i=getchar();
while(i<'0' || i>'9') {if(i=='-') f=-1; i=getchar();}
while(i>='0' && i<='9') {ans=(ans<<1)+(ans<<3)+i-'0'; i=getchar();}
return ans*f;
}
int n;
double ansx,ansy,E=1e18+10,t;//E是能量,t为初始温度
struct node {
int x,y,w;
}a[1010];
double get(double x,double y) {
double sum=0;
for(int i=1;i<=n;i++) {
double dx=x-a[i].x,dy=y-a[i].y;
sum+=sqrt(dx*dx+dy*dy)*a[i].w;
//计算势能,势能又与重物质量成正比
//根据物理知识,重物平衡时总能量最小,而此时物体动能为0,则重力势能最小时系统平衡
}
return sum;
}
void work() {
t=1024.0;//曾经沧海难为水,除却巫山不是云
double mx=ansx,my=ansy;
while(t>1e-15) {
double xx=mx+(rand()*2-RAND_MAX)*t;//得到的答案就是(-RAND_MAX,RAND_MAX),从负到正,可以多方向扩展
double yy=my+(rand()*2-RAND_MAX)*t;
double newans=get(xx,yy);//统计当前势能
double DE=newans-E;
if(DE<0) {//如果当前解更优就更新答案
ansx=xx; ansy=yy;
mx=xx; my=yy;
E=newans;
}
else if(exp(-DE/t)*RAND_MAX>rand()) {//否则我们就以一定几率来接受这个次优解,其中exp为以自然对数为底的对数函数
mx=xx; my=yy;
}
t*=delta;//降温
}
}
int main()
{
srand(time(0));
in(n);
for(int i=1;i<=n;i++) {
in(a[i].x); in(a[i].y); in(a[i].w);
ansx+=a[i].x; ansy+=a[i].y;
}
ansx/=n*1.0; ansy/=n*1.0;
for(int i=1;i<=4;i++) work();
printf("%.3lf %.3lf
",ansx,ansy);
return 0;
}