【算法简述】最短路

图论问题概述总结

对于**图论**，我们尊熟悉的算法是比较多的，这次，我就找了集中常用的算法。
## 几种算法

 1. **最短路**算法（Dijkstra,SPFE,FLOYD）

- Dijkstra单源最短算法

首先，此算法适用于计算一个点到另一个点的最短路径，且算法绝对不能出现负环。这个算法的速度慢，只用于接觉小规模的问题，如图：
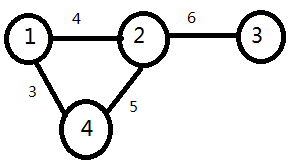这个图就是求算法的基本思路。算法过程：

 - 从节点上找到最近点那个节点，将他标记，加入集合U。
 - 将定点U连出边的邻点相连接，不在集合U中寻找。
 - 重复前面的操作，用来指导V=U是，查找结束，最后结束流程。

本算法的算法流程图：
https://wenku.baidu.com/view/8a5c11303968011ca300916a.html
参考代码：

```

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e3 + 9;
const int M = 1e4 + 9;
const int inf = 0x3f3f3f3f;
struct edge {
int v, w, next;
edge() {}
edge(int _v, int _w, int _next) {
    v = _v;
    w = _w;
    next = _next;
}
} e[M << 1];
int head[N], len;
void init() {
    memset(head, -1, sizeof head);
    len = 0;
}
void add(int u, int v, int w) {
    e[len] = edge(v, w, head[u]);
    head[u] = len++;
}
void add2(int u, int v, int w) {
    add(u, v, w);
    add(v, u, w);
}
int n, m;
int dis[N];
bool vis[N];
void dijkstra(int u) {
memset(vis, false, sizeof vis);
memset(dis, inf, sizeof dis);
dis[u] = 0;
for (int i = 0; i < n; ++i) {
    int mi = inf;
    for (int j = 1; j <= n; ++j) {
        if (!vis[j] && dis[j] < mi) {
            mi = dis[u = j];
        }
    }    
if (mi == inf) {
    return;
}
vis[u] = true;
            for (int j = head[u]; ~j; j = e[j].next) {
    int v = e[j].v;
    int w = e[j].w;
                if (!vis[v] && dis[v] > dis[u] + w) {
    dis[v] = dis[u] + w;
                }
            }
        }
    }
int main() {
init();
int u, v, w;
cin >> n >> m;
while (m--) {
    cin >> u >> v >> w;
    add2(u, v, w);
}
dijkstra(1);
cout << dis[n] << endl;
return 0;
}

```
这只是一个基本的流程代码，你可在刷掉模板的基础上，在进行修改。
**它的基本思想是以起始点为中心往外层扩展（广度优先搜索+贪心），直到扩展到终点为止。**

这就是我们的算法，因此，可以解决很多问题。

```
3 3
1 2 5
2 3 5
3 1 2
```
输入数据，看看会怎么样！ 

-堆优化Dijkstra

正对于稀疏图的算法，我们用与优化。

```

#include <iostream>
#include <cstring>
#include <set>
using namespace std;
const int N = 1e3 + 9;
const int M = 1e4 + 9;
const int inf = 0x3f3f3f3f;
typedef pair<int, int> pall;
#define X first
#define Y second
struct edge {
int v, w, next;
edge() {}
edge(int _v, int _w, int _next) {
v = _v;
w = _w;
next = _next;
}
} e[M << 1];
int head[N], len;
void init() {
memset(head, -1, sizeof head);
len = 0;
}
void add(int u, int v, int w) {
e[len] = edge(v, w, head[u]);
head[u] = len++;
}
void add2(int u, int v, int w) {
add(u, v, w);
add(v, u, w);
}
int n, m;
int dis[N];
bool vis[N];
void dijkstra(int u) {
memset(vis, false, sizeof vis);
memset(dis, inf, sizeof dis);
dis[u] = 0;
}
int main() {
init();
int u, v, w;
cin >> n >> m;
while (m--) {
cin >> u >> v >> w;
add2(u, v, w);
}
dijkstra(1);
cout << dis[n] << endl;
return 0;
}

```
找最小值，这里是和普通 Dijkstra 的核心不同之处，我们只需要获取堆顶元素即可（堆自动实现排序，
堆顶元素就是我们需要的最小值）。然后我们把这个元素加入集合（标记就是加入集合的意思）。
 

- SPFA单源最短路算法

在 SPFA 算法中，使用 di表示从源点到顶点 i的最短路，额外用一个队列来保存即将进行拓展的顶点
列表，并用ingi 来标识顶点 i是不是在队列中。
如图：
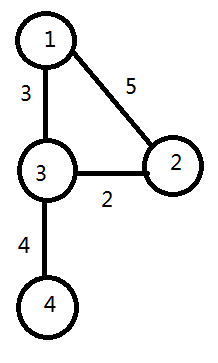
SPFA 的空间复杂度为O(V),有点像这个稀疏图的步揍。他用队列来运行，因此，SPEA只是是在对列上升级以下，并不是那种十分多的。**在一定程度上，可以认为 SPFA 是由 BFS 的思想转化而来。从不含边权或者说边权为 个单位长度的图上的 BFS，推广到带权图上，就得到了 SPFA。**

    算法步揍：
 - 用一个队列来保存多个扩展的队列。
 - 用一个队列中取的一个元素，并且对其他点进行松弛。
 - 当所有不在队列的点都入了队列，则程序结束，算法进行完毕。

```

bool inq[MAX_N];
int d[MAX_N]; // 如果到顶点 i 的距离是 0x3f3f3f3f，则说明不存在源点到 i 的最短路
void spfa(int s) {
    memset(inq, 0, sizeof(inq));
    memset(d, 0x3f, sizeof(d));
d[s] = 0;
inq[s] = true;
queue<int> q;
q.push(s);
while (!q.empty()) {
    int u = q.front();
    q.pop();
    inq[u] = false;
    for (int i = p[u]; i != -1; i = e[i].next) {
        int v = e[i].v;
        if (d[u] + e[i].w < d[v]) {
            d[v] = d[u] + e[i].w;
            if (!inq[v]) {
                q.push(v);
                inq[v] = true;
                }
            }
        }
    }
}
```
算法的图：https://i.loli.net/2019/06/09/5cfcb3db1267062487.jpg
上面的代码就是SPEA的全部结构，初始化与第一个算法一样的结构一样的。
**判断负环**的SPEA算法：

```
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e3 + 9;
const int M = 1e4 + 9;
const int inf = 0x3f3f3f3f;
struct edge {
    int v, w, next;
    edge() {}
    edge(int _v, int _w, int _next) {
        v = _v;
        w = _w;
        next = _next;
}
} e[M << 1];
int head[N], len;
void init() {
    memset(head, -1, sizeof head);
    len = 0;
}
void add(int u, int v, int w) {
    e[len] = edge(v, w, head[u]);
    head[u] = len++;
}
void add2(int u, int v, int w) {
    add(u, v, w);
    add(v, u, w);
}
int n, m;
int main() {
init();
int u, v, w;
cin >> n >> m;
while (m--) {
    cin >> u >> v >> w;
    add2(u, v, w);
}
return 0;
}

```
接下来就可以运行程序了：
```
3 3
1 2 5
2 3 5
3 1 2
``` 

- Floyd 多源最短路算法

Floyd 算法是一种计算给定的带权图中任意两个顶点之间最短路径的算法。相比于重复执行多次单源最
短路算法，Floyd 具有高效、代码简短的优势，在解决图论最短路题目时比较常用。
**floyd 算法是解决负环（可以计算出任意两点之间的最短路）有向图或无向图的多源最短路问题。常
用邻接矩阵存储，算法的时间复杂度 O(N2)，空间复杂度O(N2) 。**

算法方式：

 - 如果不经过第 个点，那么就是 dp[k-1][i][j]。
 - 如果经过第 个点，那么就是 dp[k-1][i][j]+dp[k-1][i][j]。

所以就变成了：

```

dp[k][i][j] = min(dp[k − 1][i][j], dp[k − 1][i][k] + dp[k − 1][k][j])

```
所以就变成了如下的代码：

```

int g[N][N]; // 邻接矩阵存图
int dp[N][N][N];
void floyd(int n) {
    for (int k = 0; k <= n; ++k) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (k == 0) {
                    dp[k][i][j] = g[i][j];
                } else {
                    dp[k][i][j] = min(dp[k - 1][i][j], dp[k - 1][i][k] + dp[k - 1][k][j]);
                }
            }
        }
    }
}
```
我们写出最终的 Floyd 的形式，这也是常用的写法，优化了一维的空间。并且写法更加简单。这里要注
意，枚举的中间点 一定要写在最外面。没有注意这一点，很容易把 3 个循环的顺序弄错了，那么结
果也就是错的。
刚才的分析得出：

```
int g[N][N];
void floyd(int n) {
    for (int k = 1; k <= n; ++k) {
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= n; ++j) {
                g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
            }
        }
    }
}

```
算法到这里就完成了，接下来给大家介绍**差分约束系统**。

 -  差分约束系统

我们在求解差分约束系统时，可以将其转化为图论中单源最短路（或最长路）问题。
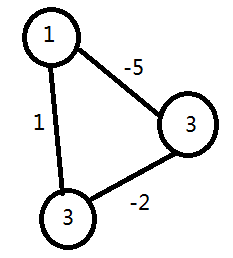
途中有负环是，就可以这样。

```

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e3 + 9;
const int M = 1e4 + 9;
const int inf = 0x3f3f3f3f;
struct edge {
    int v, w, next;
    edge() {}
    edge(int _v, int _w, int _next) {
        v = _v;
        w = _w;
        next = _next;
    }
} e[M << 1];
int head[N], len;
void init() {
    memset(head, -1, sizeof head);
    len = 0;
}
void add(int u, int v, int w) {
    e[len] = edge(v, w, head[u]);
    head[u] = len++;
}
void add2(int u, int v, int w) {
    add(u, v, w);
    add(v, u, w);
}
int n, m;
int dis[N], in[N];
bool vis[N];
bool spfa(int u) {
    memset(vis, false, sizeof vis);
    vis[u] = true;
    memset(dis, -1, sizeof dis);
    dis[u] = 0;
    memset(in, 0, sizeof in);
    in[u] = 1;
    queue<int> q;
    q.push(u);
    while (!q.empty()) {
        u = q.front();
        q.pop();
        vis[u] = false;
        for (int j = head[u]; ~j; j = e[j].next) {
            int v = e[j].v;
            int w = e[j].w;
            if (dis[v] < dis[u] + w) { // 求最长路，和求最短路相反
                dis[v] = dis[u] + w;
                if (!vis[v]) {
                    q.push(v);
                    vis[v] = true;
                    ++in[v];
                    if (in[v] > n + 1) {
                        return true;
                }
            }
        }
    }
}
return false;
}
int main() {
init();
int u, v, w, op;
cin >> n >> m;
while (m--) {
    cin >> op;
    cin >> u >> v >> w;
}
if (op == 1) {
    add(u, v, -w);
}else if (op == 2) {
    add(v, u, w);
}else {
    add(u, v, -w);
    add(v, u, w);
}
for (int i = 1; i <= n; ++i) {
    add(0, i, 0);
}
if (spfa(0)) {
    cout << "no" << endl;
}else {
    for (int i = 1; i <= n; ++i) {
        cout << "x" << i << " = " << dis[i] << endl;
    }
}
return 0;
}

```
这就是差分约束，现在运行你的程序：

```
4 3
1 1 2 3
2 3 2 2
3 3 4 1
```
~~点个赞呗~~

**本期图论结束，下期再见！**