Harris特征点检测
openCV的安装
之前没有接触过openCV的小伙伴需要先在自己的环境下进行安装,因为笔者使用的是Mac系统和Anaconda环境,所以下面这个方案是面向Mac用户的。
# Mac系统中Anaconda下安装opencv
pip install opencv-python -i https://pypi.tuna.tsinghua.edu.cn/simple
# 检测是否安装成功
import cv2
基本概念
想要学习角点检测,首先应该知道什么是角点,它的应用场景,以及如何检测某个像素点是否为角点。
角点
严格的说,角点是物体边缘的拐点。在日常生活中,绝大多数的物体都是有棱角的,例如塔尖、三角形的顶角。那么这些有转折的,或者两个物体的交接处,都可以称作是角点。
但实际上,角点到目前为止都还没有明确的数学定义,所以我们只需要简单地认为角点是一个局部极值点,或者是二维图像亮度变化剧烈的点或图像边缘曲线上曲率的极大点。
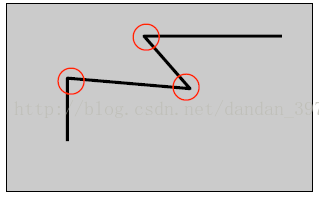
应用
角点在如今已经广泛使用,如三维重建、图像匹配等工作。
如何判断角点
- 以该像素点为中心,初始化一个滑动窗口(如3 ( imes) 3的滤波核),对它进行不同方向上的小范围移动(上下、左右、对角线),观察窗口内的像素灰度值变化情况。
- 若无论怎么移动(滑动窗口内部始终包含此像素点),内部的像素值均无变化,或者变化很小,那么表明该点是一个平坦点(flat)。
- 若此区域内的像素值在移动的过程中,在某个方向上的变化较大(单一方向),表明该点是个边缘点(edge)。
- 若该区域内的像素值在移动的过程中,对多个方向上的像素值变化都很明显,则说明这个点是个角点(corner)。
- 上述表述中的“明显”显然是我们主观的定义,那么到底多大的变化才算明显呢?我们需要对变化结果值经过一定的处理后得到最终结果(T),并对它做一个阈值处理,假设此时的阈值为(K),那么当(T > K)时,则该像素点为角点。
模型搭建与理解
前面我们已经从概念上理解了角点是什么,同时也明白了角点与普通像素点在邻域窗口中变化结果的不同。那么,到底应该具体化地表示移动下的窗口内部像素变化呢?这就涉及了数学建模的过程。
下面,我们给出在此邻域窗口内的像素灰度变化计算表示:
模型元素
已知(x, y)分别为该像素点的横纵坐标,(u, v)是窗口在水平、数值方向上的偏移。此时上述公式可拆解为四部分:
(E(u, v)):表示平移后的窗口内部像素变化值。假设此时的窗口是(3 imes 3)的滤波核,那么(E(u, v))就等于9个像素点的灰度变化之和。
(w(x, y)):窗口内各像素的权重。比较常用的是高斯核,此时考虑的是若该像素点为角点,那么它的移动一定使得灰度差值很大,所以该点的差值理应比其他点所占的权重更大。
(I(x, y)):函数(I)可求得某坐标处的像素点的灰度值。所以此时求得的是坐标为((x, y))时的灰度值。
(I(x+u, y+v) - I(x, y)):移动后对应像素的变化值。比如,此时该邻域窗口朝右下方移动,有(u = 1, v = 1),那么对于中心点的灰度变化为 (I(x+1, y+1) - I(x, y))。
⚠️ 之所以在差值外加上平方,是因为在计算过程中,我们并不能保证所有的差值都是正数,可能会出现负值。但实际上我们并不关心它的正负性,所以加平方后的求和可以消除这一影响。
公式推导
首先要明确一个目的,就是我们想要寻找一个像素点,使得我们的(u, v)无论怎样取值,(E(u, v))都是变化比较大的,这个像素点就是我们要找的角点。显然现在的公式无法让我们直观地看出在什么条件下,可以使得该值尽可能地大,因此我们将使用泰勒公式对其进行一定的化简,然后变形。
将(I(x+u,y+v)=I(x,y)+uI_x+vI_y)带入上述公式,得到
其中(I_x=frac{partial I(x,y)}{partial x}),(I_y=frac{partial I(x,y)}{partial y}) 。
提出公式内部的(u, v)后得到:
将求和公式移入矩阵内部,得到
所以最后得到:
那么这时,成功将该模型的数值变化与(M)的变化相关联。在(u,v)值不变的情况下,(E(u, v))受(M)的影响较大。
在线性代数中,有概念:实对称矩阵可以正交相似对角化。那么根据公式4,我们知道(M)是一个实对称矩阵,所以有以下变形:
且其中(P)是正交矩阵,有性质如下:
综合公式5、6、7,可以得到
所以,我们终于可以得到结果,(E(u, v))实际上就是一个椭圆呀,且根据咱们高中的知识,知道横轴是(lambda{min}^{-frac{1}{2}}),纵轴为(lambda{max}^{-frac{1}{2}})。如下图所示:
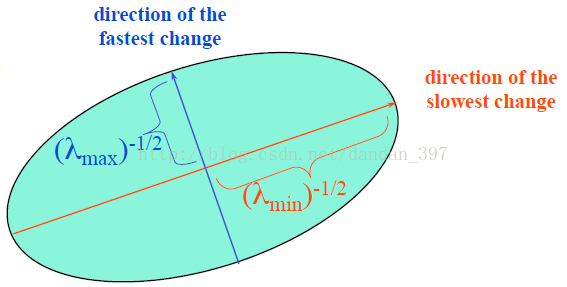
那么,前面提到我们的目标是找到一个像素点使得(E(u, v))最大,经过化简后,我们的目标转换成了找到一组(lambda_1, lambda_2)使得椭圆最大。
角点检测函数
这节就来讨论一下如何使得椭圆最大吧。从高中知识来看,显然当该椭圆的横纵轴同时很大时,它才会是最大的。那么,怎样的函数才能确保当且仅当(lambda_1, lambda_2)同时很大的情况下,函数值是最大的呢?
在这里我们定义下列公式:
其中det表示矩阵行列式,trace表示矩阵的迹。
随后,即可定义我们的角点检测函数为:
在这个公式中,k值的设定是openCV中的预设,大概也经过大量实验之后得到的“经验”值。我们将借助这个角点检测函数,对一个像素点是否为角点做一个最终判定。
角点的最终判定
在实际的角点判定中,应该假设一个适当的阈值(K)。当我们求得的(T > K)时,该像素点将被认为是一个角点。
由于结构张量(M)是由(I_x,I_y)构成,它与特征值成正比关系,那么其特征值正好可以反映两者的情况。特征值 (λ_1) 和(λ_2)决定了 T 的值,所以我们可以用特征值来决定一个窗口是平面、边缘还是角点,如下图所示:
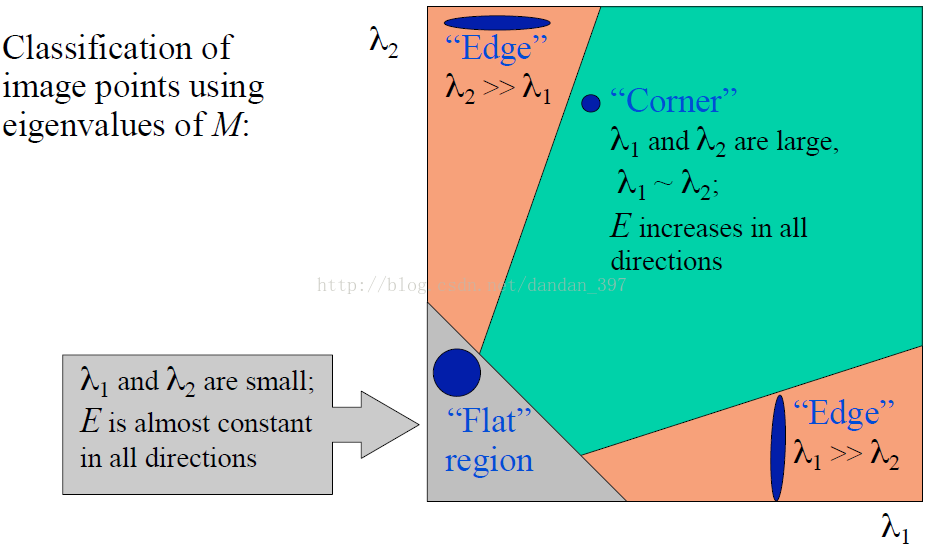
前面提到,实际上(E(u, v))的分布就像是一个椭圆,可能从这张图还不能清楚的看出,那么就借助下面这张实验结果图具体展示一下吧!
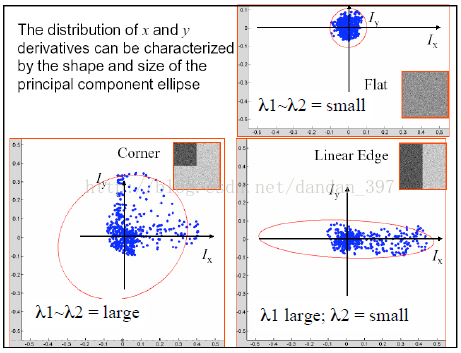
-
右上角的图中(I_x,I_y)都比较小,也就是(λ_1) 和(λ_2)都较小,红色实线框住了所有的蓝点,发现它大体是一个面积较小的圆。
-
右上角的图中(I_x,I_y)都比较大,也就是(λ_1) 和(λ_2)都较大,发现它是一个面积较大的、接近圆形的椭圆。
-
右上角的图中(I_x > I_y),也就是(λ_1 > λ_2),发现它是一个扁平的椭圆,且横轴在X轴上。
那么现在,根据上述实验结果与分块图,可以总结如下结论,假设现在有阈值(K):
-
若(lambda_1、lambda_2)都很小,使得(0< T < K),表示那么图像窗口在所有方向上的移动都无明显的灰度变化,所以该点被认为是处在平面上。
-
若(lambda_1 >> lambda_2 || lambda_2 >> lambda_1),使得(T < 1),表明图像窗口仅在水平或竖直方向有较大的变化量,所以该点被认为是处在边缘处。
-
若(lambda_1、lambda_2)都很大,使得(T > K),表示那么图像窗口在各方向上的移动灰度变化明显,所以该点被认为是角点。
代码实现
导入环境包
在进行角点检测的过程中,我们需要使用的是以下几个环境包,主要负责图像的读取和显示。
import cv2
import matplotlib.pyplot as plt
import numpy as np
读取图片
我将希望进行检测的图片放在img包下,并使用cv2的cv2.imread()方法进行读取。
img = cv2.imread("../img/cv_1.jpg")
print(img.shape) # (450, 720, 3)

灰度转换与角点检测函数
在opencv中有提供实现 Harris 角点检测的函数 cv2.cornerHarris,我们直接调用的就可以,非常方便。
函数原型:cv2.cornerHarris(src, blockSize, ksize, k[, dst[, borderType]])
对于每一个像素 (x,y),在 (blockSize x blockSize) 邻域内,计算梯度图的协方差矩阵 (M(x,y)),然后通过上面第二步中的角点响应函数得到结果图。图像中的角点可以为该结果图的局部最大值。
即可以得到输出图中的局部最大值,这些值就对应图像中的角点。
参数解释:
- src - 输入灰度图像,float32类型
- blockSize - 用于角点检测的邻域大小,就是上面提到的窗口的尺寸
- ksize - 用于计算梯度图的Sobel算子的尺寸
- k - 用于计算角点响应函数的参数k,取值范围常在0.04~0.06之间
block_size = 2
sobel_size = 3
k = 0.04
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 转化为灰度图
gray = np.float32(gray)
dst = cv2.cornerHarris(gray, block_size, sobel_size, k)
阈值设定
此次我们将阈值设置为图片中所有像素点中最大灰度值的0.01倍。假如某点灰度大于该值,则直接将颜色修改为[0, 0, 255],为红色点。
img[dst > 0.01 * dst.max()] = [0, 0, 255]
结果显示
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) # 重新转化为彩色图
plt.imshow(img)
plt.show()
最后结果如下图所示(可能需要放大才能看清...):
