题目大意
小Hi最近对生成树(包含所有顶点的联通无环子图。)非常的感兴趣,他想知道对于特定的简单平面无向图是不是存在求生成树个数的简单方法。
小Hi定义了这样的图:一个以{0,1,2……n}为顶点的图,顶点0与其他n个顶点直接相连,对于顶点i(1 ≤ i < n),顶点i与顶点i+1连有一条边。下面是小Hi画的图n=4的图:

请求出对于任意n,这样的图的生成树个数。
输入
多组数据,每组数据一行,包括一个整数n
30%的数据(1 ≤ n ≤ 100),组数不超过10组
70%的数据(1 ≤ n ≤ 1000000),组数不超过10组
100%的数据(1 ≤ n ≤ 1000000000),组数不超过10组
输出
每组数据输出一个行包括一个整数,代表了图的生成树个数(对1000000007取模)。
------------------------------------------------------------------------------------------------------------------------------
开始找错了规律,如下图,以为每加一就翻倍,却忘记了右边红框中的两种情况。
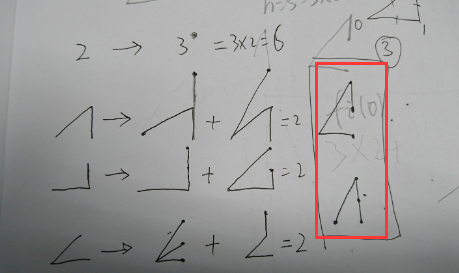
唉,考虑问题不全面。
正确的递推公式为:
令:
F(i,0) 为i是孤立的或者(仅与i-1相连)。
F(i,1) 为包括i在内的点全部联通
则
F(i+1,1) = F(i,1)*2 + F(i,0);
F(i+1,0) = F(i,1) + F(i,0);
#include <cstdio> #include <iostream> #include <algorithm> using namespace std; typedef long long LL; #define MOD 1000000007 struct Mat{ LL data[2][2]; static Mat unit(){ Mat mat; mat.data[0][0]=mat.data[0][1]=mat.data[1][0]=1; mat.data[1][1]=2; return mat; } static Mat eye(){ Mat mat; mat.data[0][0] = mat.data[1][1] = 1; return mat; } Mat(){ data[0][0]=data[0][1]=data[1][0]=data[1][1]=0; } Mat operator* (const Mat& another) const{ Mat ret; ret.data[0][0]=(data[0][0]*another.data[0][0]%MOD+data[0][1]*another.data[1][0]%MOD)%MOD; ret.data[0][1]=(data[0][0]*another.data[0][1]%MOD+data[0][1]*another.data[1][1]%MOD)%MOD; ret.data[1][0]=(data[1][0]*another.data[0][0]%MOD+data[1][1]*another.data[1][0]%MOD)%MOD; ret.data[1][1]=(data[1][0]*another.data[0][1]%MOD+data[1][1]*another.data[1][1]%MOD)%MOD; return ret; } }; LL pown(int n){ Mat unit = Mat::unit(); Mat ret = Mat::eye(); while(n){ if(n&1) ret = ret * unit; n>>=1; unit = unit * unit; } return (ret.data[1][0]+ret.data[1][1])%MOD; } int main(){ int n; while(scanf("%d",&n)!=EOF){ if(n==1) puts("1"); else{ printf("%lld ",pown(n-1)); } } return 0; }