一、二叉查找树:
查找树是一种数据结构,它支持多种动态集合操作,包括search,minimum,maximum,predecessor,successor,insert以及delete。
在二叉查找树上执行的基本操作时间与树的高度成正比。对于一棵含有n个结点的完全二叉树,这些操作的时间复杂度为O(log2n)。但是,如果树是含有n个结点的线性链,则这些操作的最坏情况下的运行时间为O(n)。
(一)二叉查找树的概念:
二叉查找树(BST,Binary Search Tree)又称二叉排序树或二叉搜索树,它或者是一棵空树,或者是一棵具有如下性质的非空二叉树:
(1)若它的左子树不空,则左子树上所有节点的值均不大于它的根节点的值;
(2)若它的右子树不空,则右子树上所有节点的值均不小于它的根节点的值;
(3)它的左、右子树也分别为二叉查找树。
等价定义:若以中序遍历二叉查找树,则会产生一个所有节点关键字值的递增序列。
例如:右下图的树,中序遍历得到的数值为(3,12,24,37,45,53,61,78,90,100)。
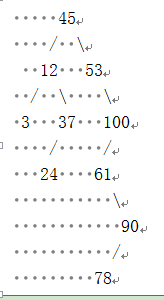
二叉查找树之所以又称为二叉排序树,因为它是“排过序”的二叉树,但并非是“用于排序”的二叉树。
不难发现,二叉查找树这种数据结构的优势在于它的有序性,这是其它类似功能的数据结构无法达到的。比如有序线性表虽然有序,但是插入算法的时间复杂度为O(n);堆的插入算法虽然时间复杂度为O(log2n),但是堆并不具有有序性。因此,我们要充分发挥二叉查找树的优势,就要充分利用其有序性和插入、查找算法的高效性。所以,如果要经常对有序数列进行“动态”的插入或查找工作,就可以采用二叉查找树来实现。
依据二叉查找树的定义,我们知道:具有相同结点集的二叉查找树,可能的形态很不同。例如对于集合{1,2,3}所建立的二叉查找树就可能是下图所示的五种形态的任一种。
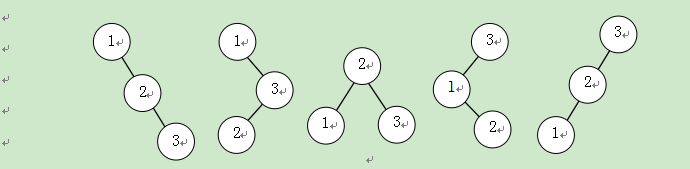
(二)二叉查找树的数据结构
一棵二叉查找树是按二叉树结构来组织的。这样的树可以用链表结构表示,其中每一个结点都是一个对象。结点中除了key域和卫星数据域外,还包含域left,right和p,它们分别指向结点的左儿子、右儿子和父结点。如果某个儿子结点或父结点不存在,则相应域中的值即为NIL。根结点是树中唯一父结点域为NIL的结点。
一般情况下,一棵二叉查找树的存储结构如下:
type node = record
key : longint; {关键值}
left, right, p : longint; {左儿子、右儿子、父结点}
…… {根据需要增加一些数据域}
end;
var bst : array[1..maxn] of node;
(三)二叉查找树的遍历
根据二叉查找树的性质,若要求按递增顺序输出树的所有关键字,只需要采用中序遍历算法递归即可:
procedure inorder_print(root : integer); {递归中序输出,从小到大}
begin
if bst[root].left<>0 then inorder_print(bst[root].left);
write(bst[root].key, ' ');
if bst[root].right<>0 then inorder_print(bst[root].right);
end;
也可以用广义表的形式输出:
procedure out(root : integer);
begin
write('(');
if bst[root].left<>0 then out(bst[root].left);
write(bst[root].key);
if bst[root].right<>0 then out(bst[root].right);
write(')');
end;
二叉查找树看似简单,且没有太多的规则,其实它在题目中变化无常,所以要真正要用好它,是需要下一番功夫的。首先要熟练掌握好它的各种基本操作,下面一一给出。
二、查询二叉查找树
对于二叉查找树,最常见的操作是查找树中的某个关键字。除了search操作外,二叉查找树还能支持诸如minimum、maximum、predecessor和successor等查询。本节就来讨论这些操作,并说明对于高度为h的树,它们都可以在O(h)时间内完成。
(一)查找关键字值为k的节点
从树的根节点出发,查找关键字k的位置。由于二叉查找树本身的特点,所以这个查找过程总是沿着树的某条路径,逐层向下进行判断比较,或者找到匹配对象,返回k值的位置;或者找不到匹配对象,返回0。递归算法如下:
function search(root, k : integer) : integer;
begin
if (root=0) or (k=bst[root].key) then exit(root);
if k<bst[root].key
then search:=search(bst[root].left, k)
else search:=search(bst[root].right, k);
end;
从算法中可以看出,这个算法递归时一旦返回,就再也不会出现递归调用,这种递归叫做末尾递归。末尾递归可以写成非递归的形式,这样可以节省栈所用的空间与运行时间。相比较递归算法而言,非递归算法更加高效:
function search(root, k : integer) : integer;
begin
while (root<>0) and (k<>bst[root].key) do
if k<bst[root].key then root:=bst[root].left
else root:=bst[root].right;
search:=root;
end;
(二)求最小(大)关键字值的结点
要查找二叉树中具有最小关键字的结点,只要从根结点出发,沿着各结点的left指针查找下去,直到遇到NIL时为止。
下面给出从树的某个结点出发,查找其子树中最小关键字值的结点位置的函数。
function min(x : integer) : integer;
begin
while bst[x].left<>0 do x:=bst[x].left;
min:=x;
end;
二叉树的性质保证了上述函数的正确性。如果一个结点x无左子树,其右子树中的每个关键字都至少和key[x]一样大,则以x为根的子树中,最小关键字就是key[x]。如果结点x有左子树,因其左子树中的关键字都不大于key[x],而右子树中的关键字都不小于key[x],因此,在以x为根的子树中,最小关键字可以在以left[x]为根的左子树中找到。
同样地,要查找二叉树中具有最大关键字的结点,只要从根结点出发,沿着各结点的right指针查找下去,直到遇到NIL时为止。这个过程与查找最小关键字的结点是对称的。
下面给出从树的某个结点出发,查找其子树中最大关键字值的结点位置的函数:
function max(x : integer) : integer;
begin
while bst[x].right<>0 do x:=bst[x].right;
max:=x;
end;
(三)求一棵二叉查找树中结点x的后继(前趋)结点。
给定一个二叉查找树中的结点,有时候要求找出在中序遍历顺序下它的后继(前驱)。如果所有的关键字都不相同,则某一个结点x的后继结点即具有大于key[x]中的关键字中最小者的那个结点。根据二叉查找树的结构,不用对关键字做任何比较,就可以找到某个结点的后继。
查找结点x的后继时需要考虑两种情况:
(1)如果结点x的右子树非空,则x的后继即右子树中的最左(小)结点,如下图中关键字是6的结点的后继结点是关键字为7的结点,关键字是15的结点的后继结点是关键字为17的结点。
(2)如果结点x的右子树为空,且x有一个后继y,则y是x的最低祖先结点,且y的左儿子也是x的祖先。如下图中,关键字为13的结点的后继是关键字为15的结点。为找到y,可以从x开始往上查找,直到遇到某个结点是其父结点的左儿子结点时为止(或者某个节点的值恰好比x大为止,求前趋亦同)。
下面给出查找结点x的后继结点y的函数:
function succ(x : integer) : integer;
var y : integer;
begin
if bst[x].right<>0
then y:=min(bst[x].right)
else begin
y:=bst[x].p;
while (bst[y].p<>0) and (x=bst[y].right) do
begin x:=y; y:=bst[y].p; end;
end;
succ:=y;
end;
相应地,查找结点x的前驱与后继是对称的,也需要考虑两种情况:
(1)如果结点x的左子树非空,则x的前趋即左子树中的最右(大)结点,如上图中关键字是15的结点的前驱结点是关键字为13的结点。
(2)如果结点x的左子树为空,且x有一个前趋y,则y是x的最低祖先结点,且y的右儿子也是x的祖先。如上图中,关键字为9的结点的前驱是关键字为7的结点。也就是要从x开始,往上找某个结点y,它的右儿子是x的祖先。其实,在没有左子树的情况下,如果x是右儿子,则前趋就是x的父结点。
下面给出查找结点x的前驱结点y的函数:
function pred(x : integer) : integer;
var y : integer;
begin
if bst[x].left<>0
then y:=max(bst[x].left)
else begin
y:=bst[x].p;
while (bst[y].p<>0) and (x=bst[y].left) do
begin x:=y; y:=bst[y].p; end;
end;
pred:=y;
end;
三、二叉查找树的插入与删除
插入和删除操作会引起以二叉查找树表示的动态集合的变化。要反应出这种变化,就要修改数据结构,但在修改的同时,还要保持二叉查找树性质。
(一)二叉查找树的插入
把结点z插入到二叉查找树T中,使T仍然满足二叉查找树的性质。
例如,下图是把关键字为14的结点,插入到一棵已存在的二叉查找树中的情况。从插入后的结果中可以看出:只要从根结点开始,不断沿着树枝下降即可。用指针x跟踪这条路径,而y始终指向x的父结点。根据key[z]与key[x]的比较结果,可以决定向左或者向右。直到x成为NIL时为止。这个NIL所占位置即我们想插入z的地方。
在下面描述的插入过程中,先将插入结点z的相关信息存放在bst数组的位置i上,插入结点的关键字为t。
procedure insert(i, t : integer);
var x, y : integer;
begin
y:=0; x:=1;
while (x<>0) and (bst[x].key<>0) do begin {从上往下找位置}
y:=x;
if t<bst[x].key then x:=bst[x].left
else x:=bst[x].right;
end;
bst[i].p:=y; bst[i].key:=t; {插入空树时,作为根结点}
if y>0 then
if t<bst[y].key then bst[y].left:=i
else bst[y].right:=i;
end;
上述过程也可以用递归过程实现。递归过程中x为空结点位置,y为父结点位置,i为查找树数组位置,t为待插入结点z的关键字:
procedure insert(x, y, i, t : integer);
begin
if x=0
then begin
bst[i].key:=t; bst[i].p:=y;
if t<bst[y].key then bst[y].left:=i
else bst[y].right:=i;
end
else if t<bst[x].key
then insert(bst[x].left, x, i, t)
else insert(bst[x].right, x, i, t);
end;
(二)二叉查找树的删除
二叉查找树的删除比它的插入要复杂一些,因为除了把某个结点删除外,还需要考虑几个限制:
(1)删除后,断开的二叉树需要重新链接起来。
(2)删除后,需保证二叉查找树性质不变。
(3)二叉树的高度决定效率,所以删除某个结点后,不能增加原二叉树的高度。
综合考虑上面的三个因素,针对被删除结点z的类型,可以分3种情况讨论:
(1)如果被删除结点z为叶结点,只需清空其父结点指向它的指针,再把该结点释放即可,即:
bst[bst[z].p].left:=0 或 bst[bst[z].p].right:=0。
(2)如果被删除结点z只有一个儿子,则可通过在其父结点和它的儿子结点之间建立一个链接,从而删除结点z。即若结点z无左子树,则用结点z右子树的根结点代替结点z,如下左图;若结点z无右子树,则用结点z左子树的根结点代替结点z,如下右图。
(3)如果被删除结点z的左右子树均存在,那么可以在其右子树中寻找关键字最小的结点,用它来代替被删除的结点,再把这个代替结点从原来的位置上删除;也可以在其左子树中寻找关键字最大的结点,用它来代替被删除的结点,再把这个代替结点从原来的位置上删除;还可以交替地用左子树中关键字最大的结点或者右子树中关键字最小的结点来代替被删除的结点,再把这个代替结点从原来的位置上删除。
以下是一个实现删除结点z的过程:
procedure delete(z : integer);
var x, y : integer;
begin
if (bst[z].left=0) or (bst[z].right=0)
then y:=z
else y:=succ(z); {找到要删除的结点y}
if bst[y].left<>0
then x:=bst[y].left
else x:=bst[y].right; {x是y的孩子}
if x<>0 then bst[x].p:=bst[y].p;
if bst[y].p=0
then root:=x {删除的是根}
else if y=bst[bst[y].p].left
then bst[bst[y].p].left:=x
else bst[bst[y].p].right:=x;
if y<>z then bst[z].key:=bst[y].key;
{如果结点中还有其它域,需要一并进行复制}
end;
【例1】编程输入一组不同的大于0的整数(共n个),建立一棵二叉搜索树;再输入一个整数,作为关键字,找到这个关键字所指定的结点,并将这个结点删除;最后按中序遍历输出广义表形式。
〖参考程序〗
type node = record
key : integer;
left, right, p : integer;
end;
var bst : array[1..5000] of node;
n, root : integer;
k, x : integer;
procedure insert(i, t : integer);
var x, y : integer;
begin
y:=0; x:=1;
while (x<>0) and (bst[x].key<>0) do begin
y:=x;
if t<bst[x].key then x:=bst[x].left
else x:=bst[x].right;
end;
bst[i].p:=y; bst[i].key:=t;
if y>0
then if t<bst[y].key then bst[y].left:=i
else bst[y].right:=i;
end;
procedure main;
var i, t : integer;
begin
readln(n);
for i:=1 to n do begin
read(t);
insert(i, t);
end;
readln;
readln(k);
end;
function min(x : integer) : integer;
begin
while bst[x].left<>0 do x:=bst[x].left;
min:=x;
end;
function succ(x : integer) : integer;
var y : integer;
begin
if bst[x].right<>0
then y:=min(bst[x].right)
else begin
y:=bst[x].p;
while (bst[y].p<>0) and (x=bst[y].right) do
begin x:=y; y:=bst[y].p; end;
end;
succ:=y;
end;
function search(root, k : integer) : integer;
begin
while (root<>0) and (k<>bst[root].key) do
if k<bst[root].key then root:=bst[root].left
else root:=bst[root].right;
search:=root;
end;
procedure delete(z : integer);
var x, y : integer;
begin
if (bst[z].left=0) or (bst[z].right=0)
then y:=z else y:=succ(z);
if bst[y].left<>0
then x:=bst[y].left else x:=bst[y].right;
if x<>0 then bst[x].p:=bst[y].p;
if bst[y].p=0
then root:=x
else if y=bst[bst[y].p].left
then bst[bst[y].p].left:=x
else bst[bst[y].p].right:=x;
if y<>z then bst[z].key:=bst[y].key;
end;
procedure out(root : integer);
begin
write('(');
if bst[root].left<>0 then out(bst[root].left);
write(bst[root].key);
if bst[root].right<>0 then out(bst[root].right);
write(')');
end;
begin
fillchar(bst, sizeof(bst), 0);
main;
root:=1;
x:=search(root, k);
if x<>0 then delete(x);
out(root);
end.
至此,一般的二叉查找树的基本模块介绍完毕。当然二叉查找树能帮助我们实现的远不止上述功能,我们可以通过对二叉查找树数据结构中域的改变来实现一些我们需要的操作。如查找关键字为第k大(小)的结点,我们可以增加一个count域,count[z]的值为结点z的左右子树中共有多少个结点,这样,就可以帮助我们在O(h)的时间复杂度内找出我们要找的结点。
但是二叉查找树并不一定是平衡树,它在最坏的情况下,二叉查找树可能会退化成含有n个结点的线性链(如输入结点信息时,其关键字严格按递增或递减顺序排列),此时在二叉查找树上进行的所有操作的时间复杂度都会退化达到O(n)。