<分治>
题目描述
根据一棵树的中序遍历与后序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
中序遍历 inorder = [9,3,15,20,7] 后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树:
3
/
9 20
/
15 7
我的思路
class Solution(object): def buildTree(self, inorder, postorder): """ :type inorder: List[int] :type postorder: List[int] :rtype: TreeNode """ def resolve(inorder,postorder,tar): left,right=None,None # 找到目标结点的左孩子 if tar.val in inorder and inorder.index(tar.val)-1>=0: left = inorder[inorder.index(tar.val)-1] # 找到目标结点的右孩子 if tar.val in postorder and postorder.index(tar.val)-1>=0: right = postorder[post.index(tar.val)-1] # 防止死循环 if tar.val in inorder: inorder.pop(inorder.index(tar.val)) if tar.val in postorder: postorder.pop(postorder.index(tar.val)) # 出口条件 if not left and not right or not tar: return # 链接左孩子 tar.left = TreeNode(left) # 链接右孩子 tar.right = TreeNode(right) #递归 resolve(inorder,postorder,tar.left) resolve(inorder,postorder,tar.right) ret = TreeNode(postorder[-1]) resolve(inorder,postorder,ret) return ret
-
算法
1. 先找到根节点(即目标结点)
2. 找到根节点的左孩子,即中序里面目标结点的前一个
3. 找到根节点的右孩子,即后序里面目标结点的前一个
-
存在的问题
1. 对于 [2,1],[2,1],这组数据该算法无效。
题解 - 分治思想
class Solution(object): def buildTree(self, inorder, postorder): if not inorder: return None root = TreeNode(postorder[-1]) i = inorder.index(root.val) root.left = self.buildTree(inorder[:i],postorder[:i]) root.right = self.buildTree(inorder[i+1:],postorder[i:-1]) return root
-
如何界定分治后左子树和右子树的范围?
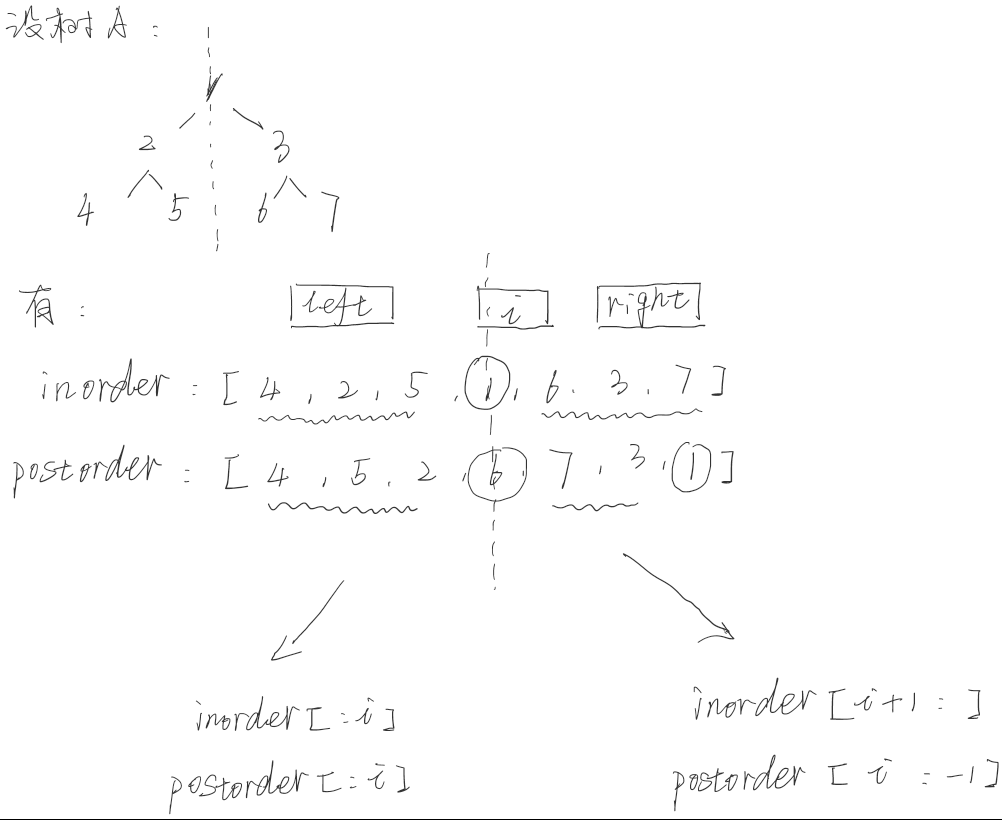
总结
-
分治思想解题
-
注意分割问题时的边界问题