116. 填充每个节点的下一个右侧节点指针

<>

题目描述

---

给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例：

输入：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":null,"right":null,"val":4},"next":null,"right":{"$id":"4","left":null,"next":null,"right":null,"val":5},"val":2},"next":null,"right":{"$id":"5","left":{"$id":"6","left":null,"next":null,"right":null,"val":6},"next":null,"right":{"$id":"7","left":null,"next":null,"right":null,"val":7},"val":3},"val":1}

输出：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":{"$id":"4","left":null,"next":{"$id":"5","left":null,"next":{"$id":"6","left":null,"next":null,"right":null,"val":7},"right":null,"val":6},"right":null,"val":5},"right":null,"val":4},"next":{"$id":"7","left":{"$ref":"5"},"next":null,"right":{"$ref":"6"},"val":3},"right":{"$ref":"4"},"val":2},"next":null,"right":{"$ref":"7"},"val":1}

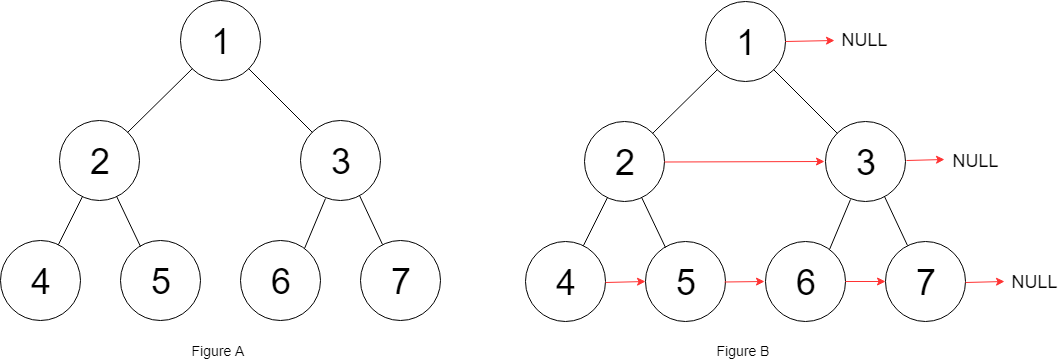
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

提示：

• 你只能使用常量级额外空间。
• 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

 

我的思路 - BFS

---

class Solution(object):
    def connect(self, root):
        """
        :type root: Node
        :rtype: Node
        """
        if not root:
            return None
        que = [root]
        while len(que):
            t = []
            for i in range(len(que)):
                if i==len(que)-1:
                    que[i].next = None
                else:
                    que[i].next = que[i+1]
                if que[i].left:
                    t.append(que[i].left)
                    t.append(que[i].right)
            que = t
        return root

•  算法：

利用层序遍历，当处在在一层的时候，把这一层的结点 “串起来” ，末尾的结点指向None即可。

• 存在的问题：

利用了一个辅助栈，花费了O(n)的空间。

• 优化的可能

不用辅助栈，改用变量来记录一层的结点数量，实现常量级额外空间

 

我的思路 - 递归

---

class Solution(object):
    def connect(self, root):
        """
        :type root: Node
        :rtype: Node
        """
        if not root:
            return 
        # 把视角切换到当前结点，我们来关心当前结点的左右孩子
        # 第一种情况：左孩子直接连接右孩子，很简单
        if root.left:
            root.left.next = root.right
            
        # 第二种情况，右孩子在树的左边，或者右孩子在树的右边
        # ① 在左边的时候，根据当前结点的next找到右边的那个结点

        # 第二种情况：处理右孩子，通过当前节点的next指针，找到右孩子的next结点。
        #           要注意判断当前结点的位置是在树的左侧还是右侧（边界）
        if root.next and root.right:
            root.right.next = root.next.left

        # ② 在右边的时候，有可能处在边界位置，把它设置为None。（多次一举，因为默认next是默认指向None的）
        elif not root.next and root.right:
            root.right.next = None
        self.connect(root.left)
        self.connect(root.right)
        return root

• 算法：