[APIO2018]铁人两项 --- 圆方树

 [APIO2018] 铁人两项

 

题目大意：

给定一张图，问有多少三元组（a,b,c）（a，b，c 互不相等）满足存在一条点不重复的以a为起点，经过b，终点为c的路径

 

如果你不会圆方树 ----------------------- 放弃是最好的选择（先学了再来吧）

如果你会圆方树

考虑((a,...,c))

1.如果a,c不同属一个点双，不难发现答案为路上经过的（点双的节点个数）的和减去割点数

2.如果a,c同属一个点双，那么答案为本点双的节点个数 - 2

自然地想到方点的权值为内含节点个数（割点算在内），圆点权值为 -1

 

所以答案就是树上的路径权值之和了。

树形DP一下就好了 ------------------------------------------- 那就是错了。。。。

 

考虑的三元组中的a,c明显指圆点，方点是不能作为路径的起点和终点的。。。。。

于是，考虑每个点能出现的路径个数。

记(sz[e])表示节点e在圆方树的子树中存在多少圆点

对于每个点，存在两种路径：

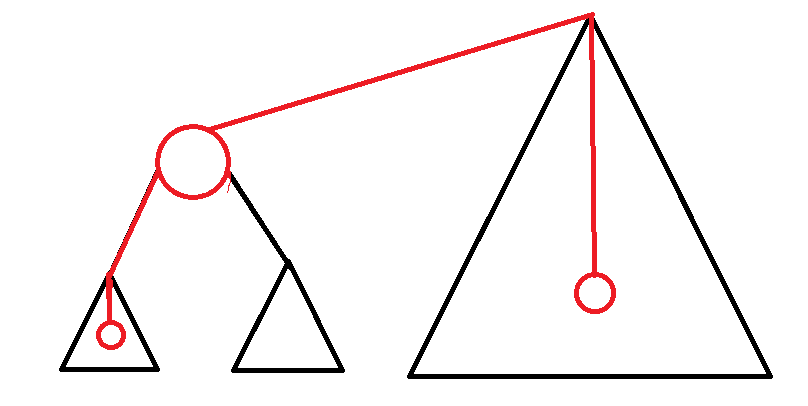
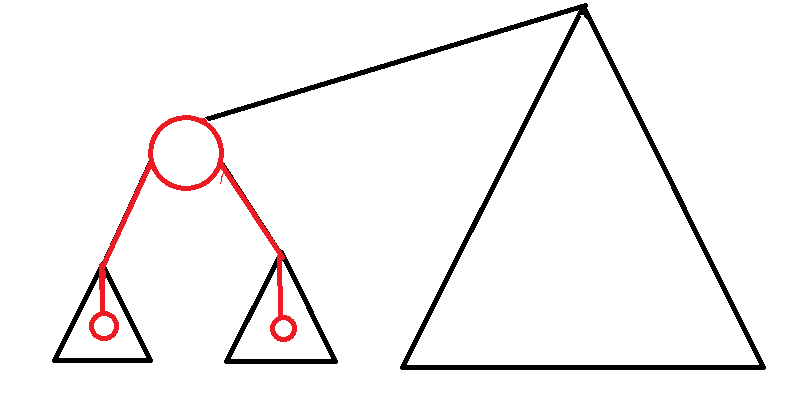
分两种情况统计即可

额外的，对于圆点，因为可能作为起点，终点，还要额外统计

莫名其妙的$loj$和$luogu$的$rk1$.......还是挺懵逼的

 

代码如下：

#include <cstdio>
#define sid 500050
using namespace std;

long long ans;
int n, m, top, tim, nt, cnt, Asz, pp;
int dfn[sid], low[sid], st[sid], sz[sid], val[sid];
int cap[sid], acap[sid], nxt[sid], node[sid];

int read() { scanf("%d", &pp); return pp; }
void upmin(int &a, int b) { if(a > b) a = b; }
void Add(int u, int v) { nxt[++ cnt] = cap[u]; cap[u] = cnt; node[cnt] = v; }
void Bdd(int u, int v) { nxt[++ cnt] = acap[u]; acap[u] = cnt; node[cnt] = v; }

void Tarjan(int e) {
    dfn[e] = low[e] = ++ tim;
    st[++ top] = e; sz[e] = 1; val[e] = -1;
    for(int i = acap[e], d; i; i = nxt[i])
    if(!dfn[d = node[i]]) {
        Tarjan(d); upmin(low[e], low[d]);
        if(low[d] < dfn[e]) continue;
        int p; ++ nt; Add(e, nt);
        do {
            p = st[top --]; val[nt] ++;
            Add(nt, p); sz[nt] += sz[p];
        } while(p != d);
        val[nt] ++; sz[e] += sz[nt];
    }
    else upmin(low[e], dfn[d]);
}

void DP(int e) {
    if(e <= n) ans += 1ll * (Asz - 1) * val[e];
    ans += 1ll * (Asz - sz[e]) * sz[e] * val[e];
    for(int i = cap[e]; i; i = nxt[i]) {
        int d = node[i];
        DP(d), ans += 1ll * (Asz - sz[d]) * sz[d] * val[e];
    }
}

int main() {
    nt = n = read(); m = read();
    for(int i = 1; i <= m; i ++) {
        int u = read(), v = read();
        Bdd(u, v); Bdd(v, u);
    }
    for(int i = 1; i <= n; i ++)
    if(!dfn[i])
    Tarjan(i), Asz = sz[i], DP(i);
    printf("%lld
", ans);
    return 0;
}