文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准。感谢博主Rachel Zhang的个人笔记,为我做个人学习笔记提供了很好的参考和榜样。
§ 1. 单变量线性回归 Linear Regression with One Variable
1. 代价函数Cost Function
在单变量线性回归中,已知有一个训练集有一些关于$x$、$y$的数据(如×所示),当我们的预测值$h(x)$被假设为$h(x)=\theta_{0}+\theta_{1}x$时,我们要使得$\theta_{0}$、$\theta_{1}$两个参数所表示的直线(蓝线)尽量与这些数据点很好地拟合。想要实现这个思路,就需要使得同一$x$对应的$h(x)$与$y$ 尽量相近。在这样的假设中,$J(\theta_{0},\theta_{1})$被称为Cost Function(也称平方误差代价函数),我们在实验过程中应该使得这一函数值尽量小。在这样的$h(x)$中,只出现了一个变量$x$,因此也叫单变量(One Variable);以后也可能会出现多变量的情况,比如$h(x_{1},x_{2})=\theta_{0}+\theta_{1}x+\theta_{2}x^{2}$
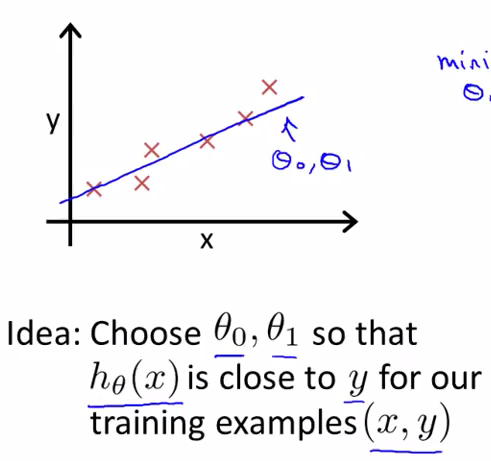

单参数的情况下非常容易理解:在这里,Andrew Ng将h(x)简化,使得$\theta_{0}=0$,只考虑$\theta_{1}$。再举例示范了一下由$J(\theta_{1})$确定$\theta_{1}$值的过程。

单参数情况下,得出的$J(\theta_{1})$是一个弓形,而当有两个参数的时候则有所不同。
有两个参数的情况下,得出的$J(\theta_{0},\theta_{1})$是一个3D的碗状图形,三个坐标轴分别代表了两个参数$\theta_{0},\theta_{1}$和代价函数$J(\theta_{0},\theta_{1})$。

但通常,我们用轮廓图(Contour Plot or Coutour Figure)来表示这样的3D模型。
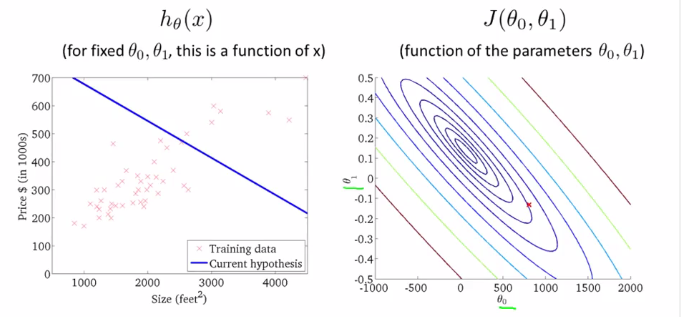
上右即为轮廓图。在同一个椭圆上的各个点,$J(\theta_{0},\theta_{1})$的值是相同的,而越靠中心的椭圆则J值越小。
2.梯度下降算法Gradient Descent
梯度下降算法被广泛运用在机器学习领域中。本章中,主要介绍利用梯度下降算法(Gradient Descent)最小化线性回归的代价函数。

1 初始设定$\theta_{0}$与$\theta_{1}$,一般将二者都初始化为0
2 不断改变$\theta_{0}$与$\theta_{1}$,使得$J$减小
3 直到找到最小值时结束
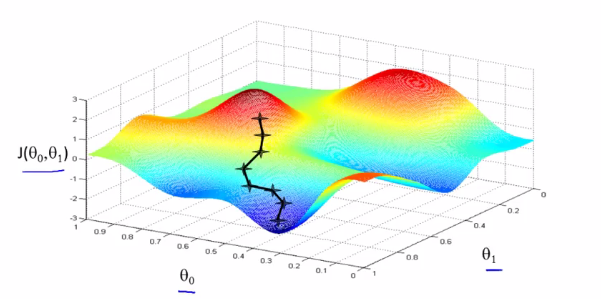
把Cost Function的图形想成山,而你在山上的某一点,那么梯度下降算法就是环顾四周,找到最快下山的路径,迈出一步,然后再环顾四周,找到最快下山的路径,再迈出一步,如此反复。
但梯度下降算法有一个特点,如果你从稍微偏一些的角度作为初始化点,那么完全可能去到另一个局部最优解的点上,与之前的完全不同。例如下图:
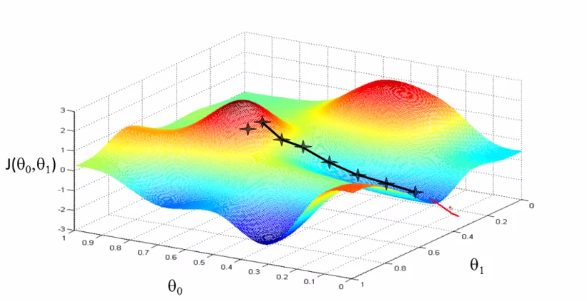
但事实上线性回归的代价函数总是一个凸函数(Convex Function),这样的函数只存在一个全局最优解,不存在有多个局部最优解的情况,所以不需要考虑这个问题。
具体的算法如下:

其中α表示学习速率(Learning Rate)表示我们以多大幅度更新theta_j

注意:我们应该像左边的情况这样实现同步更新(Simultaneous Update),否则就会出现错误。
例题(考察了一下同步更新):

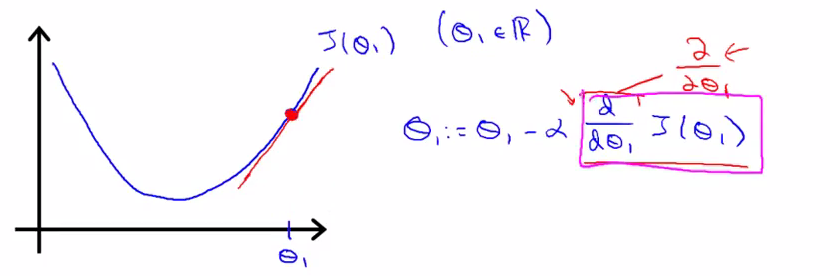
对于粉色方框里的导数项,则表示了与蓝线相切的红线的斜率。
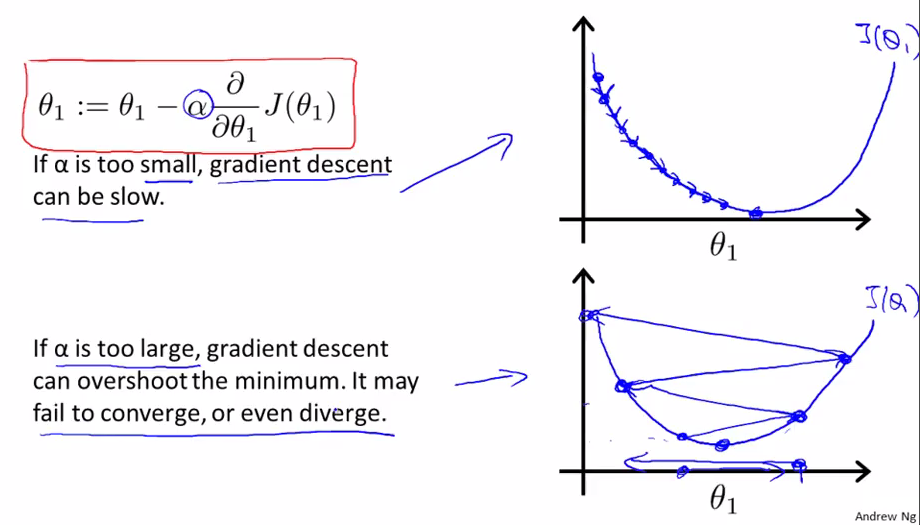
关于学习速率α,如果过小,那么梯度下降的速度会很慢;如果过大,那么可能难以收敛,甚至会发散。所以应该适当地选择α。
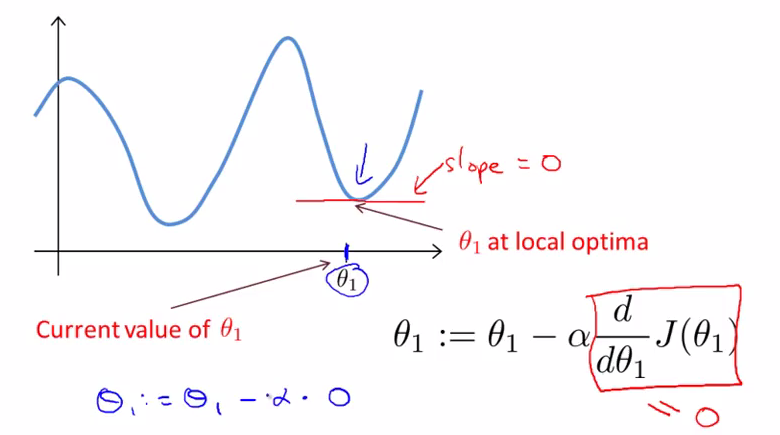
如果出现$\theta_{1}$已是局部最优解的情况,那么在那一点,它的切线斜率为0,因此$\theta_{1}$不会改变。可见,即使α不变,梯度下降算法也能找到局部最优点。
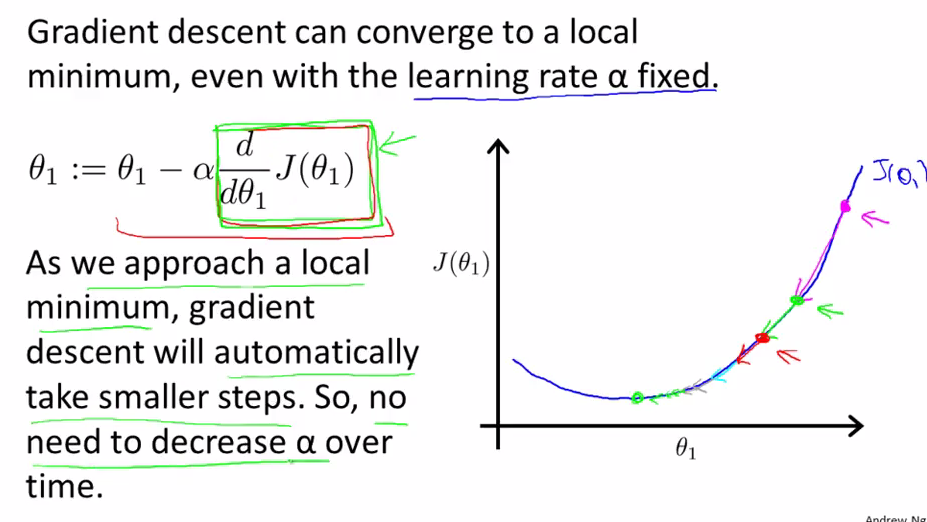
由于每接近局部最优解一些,梯度下降算法都会自动的把下降幅度变小,因此无需随之减小α
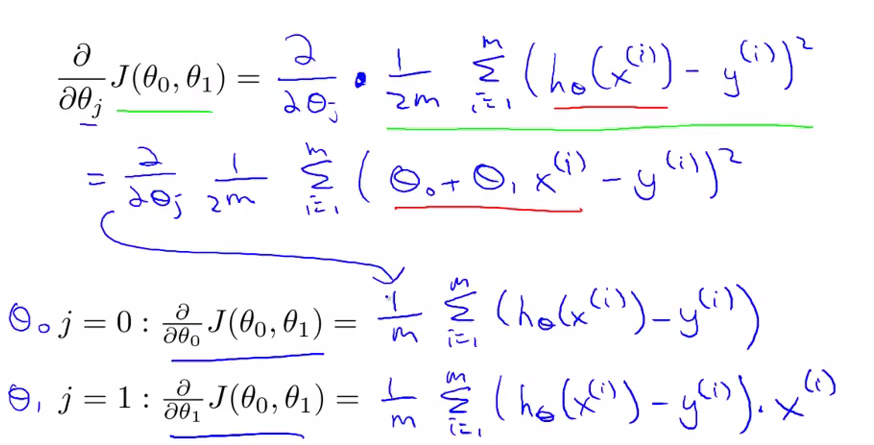
推导可得:

而后引入批量梯度下降算法的概念:即在梯度下降算法的每一步都用到了所有的训练样本。

在数据量较大的情况下,梯度下降算法比正规方程适用。
笔记目录
(一)单变量线性回归 Linear Regression with One Variable
(二)多变量线性回归 Linear Regression with Multiple Variables
(四)正则化与过拟合问题 Regularization/The Problem of Overfitting
(五)神经网络的表示 Neural Networks:Representation
(六)神经网络的学习 Neural Networks:Learning
(七)机器学习应用建议 Advice for Applying Machine Learning
(八)机器学习系统设计Machine Learning System Design
(九)支持向量机Support Vector Machines
(十)无监督学习Unsupervised Learning
(十一)降维 Dimensionality Reduction
(十二)异常检测Anomaly Detection
(十三)推荐系统Recommender Systems
(十四)大规模机器学习Large Scale Machine Learning