[Paper Review] Generative Adversarial Nets, 2014

GANs is supervised learning, so there is only X, no label y. The network tries to learn the data distribution of X, and the goal is to generate new synthetic samples that belong to this distribution. To learn the generator's distribution p_g over data X, we define a prior on input noise variables p_z(Z), then represent a mapping to data space as G(z,θ_g), where G is a differentiable function represented by a multilayer perceptron with parameters θ_g.

This process is explained very well in reference[2]: GANs seem to generate RV from multi-dimensional noise, but it actually transforms a simple RV to a much more complex RV. We can consider a RV Z as the result of a inversible operation or a process: F(X) = Z, and then X = F^-1(Z). If we know the funtion F^-1, we could transform a RV belonging to distribution X based on a RV from distribution Z.

From blue distribution(uniform) to orange distribution(Gaussian)

The generative model can be thought of as analogous to a team of counterfeiters, trying to produce fake currency and use it without detection, while the discriminative model is analogous to the police, trying to detect the counterfeit currency. Competition in this game drives both teams to improve their methods until the counterfeits are indistiguishable from the genuine articles.

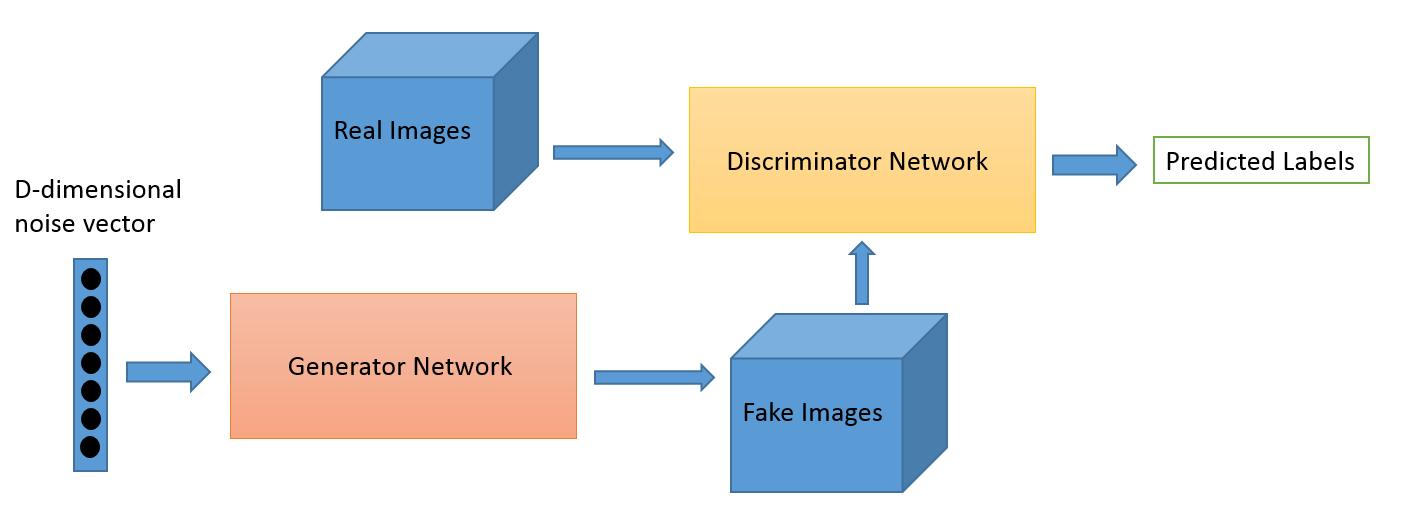
G(z) is the fake data, and D(x) represents the probability that x came from the data rather than p_g. D and G play the following two-player minimax game with value function V (G;D):

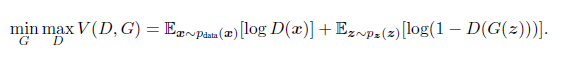
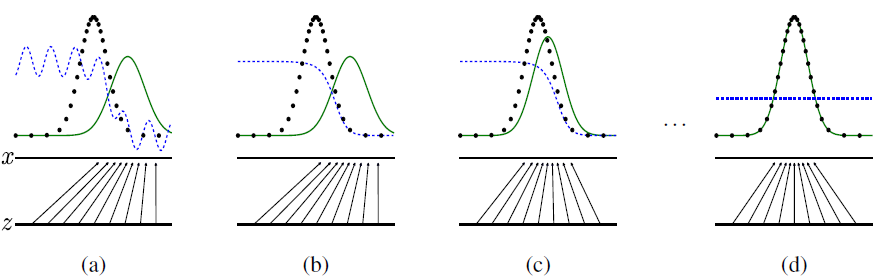
Here is the figure to show how generative model G and discriminative model D improve themselves, in which the first figure ever published in a GAN paper, illustrating a GAN learning to map uniform noise to the normal distribution. Black dots are the real data points, the green curve is the distribution generated by the GAN, and the blue curve is the discriminator’s confidence that a sample in that region is real. Here x denotes the sample space and z the latent space.

 

Reference:

[1] Goodfellow, Ian J., et al. Generative Adversarial Networks. June 2014.

[2] https://towardsdatascience.com/understanding-generative-adversarial-networks-gans-cd6e4651a29