在Batch Gradient Descent及Mini-batch Gradient Descent, Stochastic Gradient Descent(SGD)算法中,每一步优化相对于之前的操作,都是独立的。每一次迭代开始,算法都要根据更新后的Cost Function来计算梯度,并用该梯度来做Gradient Descent。
Momentum以及Nestrov Momentum相较于前三种算法,虽然也会根据Cost Function来计算当前的梯度,但是却不直接用此梯度去做Gradient Descent。而是赋予当前梯度一个权值,并综合考虑之前N次优化的梯度(使其形成一个动量、或类比为惯性),得到一个加权平均的移动平均值(Weighted Moving Average),之后再来作Gradient Descent。
Gradient Descent with Momentum:
首先,我们需要计算Momentum,即动量。这里使用Exponential Moving Average(EMA)来计算该加权平均值,公式为:
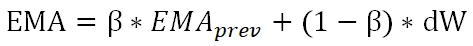
dW为本次计算出的梯度值,β是衰减因子,取值在0-1之间。为了直观的理解指数衰减权值,将上式展开,可以得到:
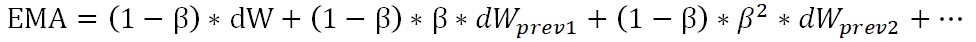
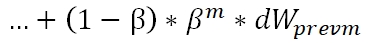
通过上式,我们可以知道,梯度序列的权重是随着β进行指数衰减的。根据β值的大小,可以得出大致纳入考虑范围的步数为1/(1-β),β值越大,衰减满、纳入考虑的步数约多,反之则窗口约窄。
Momentum算法会减小算法的震荡,在实现上也非常有效率,比起Simple Moving Average,EMA所用的存储空间小,并且每次迭代中使用一行代码即可实现。不过,β成为了除α外的又一个Hyperparameter,调参要更难了。
Nesterov Momentum:
如下图左侧所示,Gradient Descent with Momentum实际上是两个分向量的加和。一个分量是包含“惯性”的momentum,另一个分量是当前梯度,二者合并后产生出实际的update梯度。下图右侧,是Nesterov Momentum算法的示意图。其思路是:明知道momentum分量是需要的,不如先将这部分更新了。
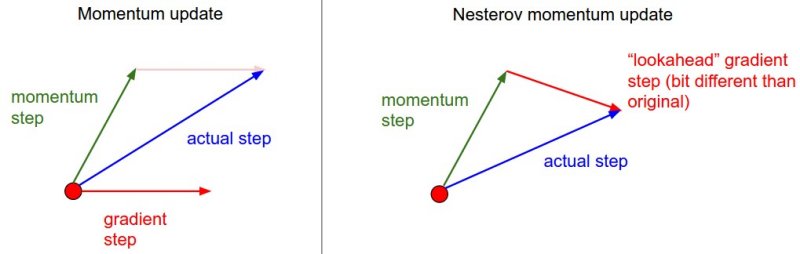
在下图中,Nesterov算法不在红点处计算梯度,而是先更新绿色箭头,并且在绿色箭头处计算梯度,再做更新。两个算法会得出不一样的结果。