在利用基本的概率论模型解决实际问题的时候,我们很容易发现一些随机变量的连续分布的,例如火车进站的时间、台灯的寿命等一些和时间相关的随机变量,此时我们发现我们难以求出某个点的概率了,因为随机变量是连续的,基本事件空间是一个无穷的空间,而与无限、连续这些字眼相关,很自然的想到,这里我们要借助积分的工具。
现在我们面临的问题是,如何用上积分这个工具呢?我们假想一条曲线f(x)和连续随机变量的取值区间[a,b]围成了一个面积为1的曲边梯形,(之所以控制面积为1,是为了满足分布列的基本性质),那么对于P(c≤X≤d),就等于f(x)在[c,d]的定积分。
容易看到对于不同问题的分布列,这样一个曲边梯形中的f(x)和分布列自身是构成一一映射的,我们称f(x)是连续随机变量X的概率密度曲线。
基于这些东西,我们可以很好地给连续随机变量下一个定义了:
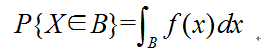
满足这样的概率分布的分布列的随机变量X成为连续性随机变量(其中B是表示取值范围的集合)。
Ex1 (uva 11346):
给出一个区域[-a,b] , [-b,b],给出面积S,问在该区域内任选一点P,使得P和坐标原点为对角线的矩形的面积大于S的概率是多少。
分析:
很典型的几何概型问题或者说连续型随机变量,这里需要注意的是,定积分求解出一个结果会出现ln,要保证ln在程序中运算有意义,所以它的真数要大于0.