Q:现在有一个长B的大桥,你在大桥上建造一系列等距的电线杆,电线杆之间的距离不得超过D,随后你将总长为L的电线挂在电线杆上形成一系列全等对称的抛物线,现在请问:当建造的电线杆最少的时候,抛物线的最低点与桥面之间的距离y。如下图。
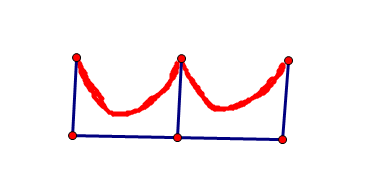
输入格式:输入第一行为测试数据组数T,接下来是4个整数D、H、B、L(B≤L)。
分析:其实这道问题的临界分析非常简单,使得电线杆最少,只需要间隔达到D即可,间隔数n=(int)B/D,间隔的距离D1=B/n,间隔内的电线长度为L1=L/n,即我们其实是解决如下的数学问题:
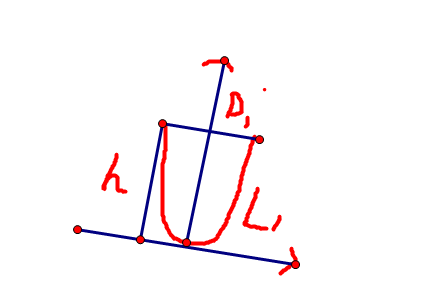
已知过原点的抛物线f(x)区间[-D1/2,D1/2]上的弧长L1,求f(D1/2),那么H-f(D1/2)便是这道问题的最终解。
设f(D1/2)=h,我们将其视为参数,得到抛物线的解析式,然后结合连续函数的求弧长公式,便可建立方程。此时存在h一个未知数,对于方程我们有很好的求根策略,适用于一切复杂的方程形式——二分法。