《训练指南》——7.24

  Uva10891:

  有一个长度为n的整数序列，两个游戏者A和B轮流取数，A先取。每次玩家只能从左端或者右端取任意的数。所有数都被取走后游戏结束， 然后统计每个人去走的所有数回合，作为格子的得分。两个人采取的策略都是让自己的得分尽量高，并且两个人足够聪明，求A的得分减去B的得分后的结果。

  分析：乍一看这是一个博弈游戏，但是我们究博弈的本质其实也是状态之间的转移。观察这道题目的参数是1~n个整数，我们将其视为一个区段，然后就很容易对区段进行子问题化，注意到这里描述某个状态，两个参量是这个区间的起点和终点，还有一个重要的参量是当前状态是A选数还是B选数，为了避免设置三维数组，这里我们统一设置dp[i][j]表示面临i~j这种情况的先手能够取得的最高分，那么很容易看到，整个游戏A取得的分数，就是dp[1][n]。

  但是现在的问题是如何利用这种描述状态的方法进一步得到状态转移方程，容易看到，对于dp[1][n]，先手A有一系列的取法，我们枚举这一系列的取法(左端取k∈[1,n-1]，右端取k∈[1,n])，然后得到A的得分，维护一个最大值就可以了，这样满足博弈的限制条件(两个人采取的策略都是让自己的分数尽量高，并且两个人足够聪明)。

                          

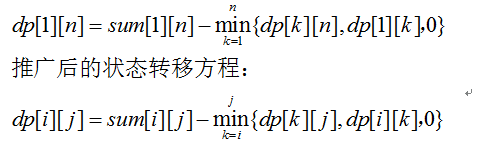
  这里需要注意的，min{}中第一项中k是从i+1开始取的，很显然k=i没有意义，因为面临[i,j]的状态的玩家必须取走一个。另外min{}中0的意义的解读，也就是说面临[i,j]状态时，当前玩家存在一个策略是取走所有的数字。确保了所有的可转移到当前状态的子状态枚举的齐全性，也就保证了动态规划过程正确性。

  简单的参考代码如下：

#include<cstdio>

#include<algorithm>

#include<cstring>

using namespace std;

const int maxn = 105;

int S[maxn],A[maxn];

int dp[maxn][maxn];

int visit[maxn][maxn];

 

int Dp(int i , int j)

{

    if(visit[i][j])   return dp[i][j];

    visit[i][j] = 1;

    int Min = 0;

    for(int k = i + 1;k <= j;k++)   Min = min(Dp(k , j) , Min);

    for(int k = i    ;k <  j;k++)   Min = min(Dp(i , k) , Min);

      dp[i][j] = S[j] - S[i-1] - Min;

      return dp[i][j];

 

}

 

 

int main()

{

        int n;

        while(scanf("%d",&n) && n)

        {

            S[0] = 0;

            memset(visit , 0 , sizeof(visit));

              for(int i = 1;i <= n;i++)

              {

                  scanf("%d",&A[i]);

                      S[i] = S[i-1] + A[i];

              }

 

             printf("%d
",2*Dp(1,n) - S[n]);

        }

}