这一章节讨论积分的定义以及微积分基本定理。
笔者先前在数学证明专栏中关于高斯定理的证明的开头,给出了一段关于微积分思想的概括,文中提到根据导数(微分)的定义,根据其逆定义来给出积分的定义和计算方法,这里其实是及其不严谨的,积分本身有着自己的定义,而其计算方法正是微积分基本定理所呈现出来的东西。
积分的定义:
积分的现代定义的本质就是黎曼和,笔者之前关于多重积分定义的引入其实就已经提到过,这里是对一维的积分进行定义,相对二重、三重积分则会简单很多。
理论总是源于实际问题嘛,在解决曲线和坐标系围成的曲边梯形的面积的问题中,我们引入的积分。
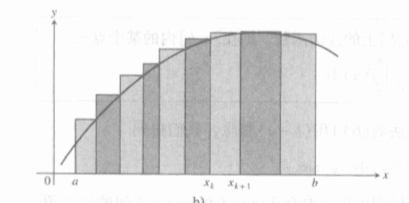
可以看到曲边梯形的面积可以近似的表示成如下的形式:
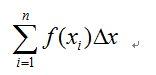
n趋于无穷之后便不再是近似相等而是严格相等。这边引入了积分符号
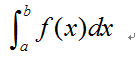
微积分的严格定义如下:

积分符号的详细解释:

依据定义我们能够得到它的如下运算性质:

充分理解积分概念对恰到好处的应用微积分非常重要,它的一个具体表现形式就是在一系列物理问题中,离散化的方程已经不能够适应我们对复杂问题的探究,这里就需要取一个积分变量dx列出存在积分的等式进行求解,而且对概念的充分理解也会有利于微积分的一系列高级应用——微分几何、偏微分、微分方程等中起到核心的作用。