Dev.C++线段树模板:在对一段区间进行修改或查询时,数组(\(n^2\))……显而易见,会爆……这时,线段树(\(nlogn\))就是一个很好的选择
老规矩,先贴代码:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll N=100100;
ll n,m,a[N];
struct tree{
ll l,r;
ll pre,add;
}t[4*N];
void build_tree(ll p,ll l,ll r){
t[p].l=l,t[p].r=r;
if( l==r ) {
scanf("&lld",&t[p].pre);
return ;
}
ll mid=(l+r)/2;
build_tree(p*2,l,mid);
build_tree(p*2+1,mid+1,r);
t[p].pre=t[p*2].pre+t[p*2+1].pre;
}
void lazy_tag(ll p){
if( t[p].add ) {
t[p*2].pre+=t[p].add*(t[p*2].r-t[p*2].l+1);
t[p*2+1].pre+=t[p].add*(t[p*2+1].r-t[p*2+1].l+1);
t[p*2].add+=t[p].add;
t[p*2+1].add+=t[p].add;
t[p].add=0;
}
}
void update(ll p,ll x,ll y,ll z){
if( x<=t[p].l && y>=t[p].r ) {
t[p].pre+=(ll)z*(t[p].r-t[p].l+1);
t[p].add+=z;
return;
}
lazy_tag(p);
ll mid=(t[p].l+t[p].r)/2;
if( x<=mid ) update(p*2,x,y,z);
if( y>mid ) update(p*2+1,x,y,z);
t[p].pre=t[p*2].pre+t[p*2+1].pre;
}
ll query(ll p,ll x,ll y){
if( x<=t[p].l && y>=t[p].r ) return t[p].pre;
lazy_tag(p);
ll mid=(t[p].l+t[p].r)/2;
ll ans=0;
if( x<=mid ) ans+=query(p*2,x,y);
if( y>mid ) ans+=query(p*2+1,x,y);
return ans;
}
int main(){
scanf("%lld%lld",&n,&m);
build_tree(1,1,n);
for(ll i=1;i<=m;i++){
ll p,x,y,k;
scanf("%lld",&p);
if( p==1 ){
scanf("%lld%lld%lld",&x,&y,&k);
update(1,x,y,k);
}
if( p==2 ){
scanf("%lld%lld",&x,&y);
printf("%lld\n",query(1,x,y));
}
}
return 0;
}
意义:在对一段区间进行修改或查询时,数组(\(n^2\))……显而易见,会爆……这时,线段树(\(nlogn\))就是一个很好的选择
使用:建立一棵二叉树,用数组存储这棵树,叶子节点就是你要存的(空间换时间)。
递归存储:
void build_tree(ll p,ll l,ll r){
t[p].l=l,t[p].r=r;
if( l==r ) {
scanf("&lld",&t[p].pre);
return ;
}
ll mid=(l+r)/2;
build_tree(p*2,l,mid);
build_tree(p*2+1,mid+1,r);
t[p].pre=t[p*2].pre+t[p*2+1].pre;
}
递归建树变量:p(数组下标),l(左端点),r(右端点)。
if( l==r ) :在它搜到叶子(左端点等于右端点)时,输入叶子数据(建树)
ll mid=(l+r)/2:二分建树
t[p].pre=t[p2].pre+t[p2+1].pre:求 祖宗 父节点
这个递归建树还是比较容易理解的哈简单到爆
先别飘哈咱还有难的呢
void lazy_tag(ll p){
if( t[p].add ) {
t[p*2].pre+=t[p].add*(t[p*2].r-t[p*2].l+1);
t[p*2+1].pre+=t[p].add*(t[p*2+1].r-t[p*2+1].l+1);
t[p*2].add+=t[p].add;
t[p*2+1].add+=t[p].add;
t[p].add=0;
}
}
void update(ll p,ll x,ll y,ll z){
if( x<=t[p].l && y>=t[p].r ) {
t[p].pre+=(ll)z*(t[p].r-t[p].l+1);
t[p].add+=z;
return;
}
lazy_tag(p);
ll mid=(t[p].l+t[p].r)/2;
if( x<=mid ) update(p*2,x,y,z);
if( y>mid ) update(p*2+1,x,y,z);
t[p].pre=t[p*2].pre+t[p*2+1].pre;
}
ll query(ll p,ll x,ll y){
if( x<=t[p].l && y>=t[p].r ) return t[p].pre;
lazy_tag(p);
ll mid=(t[p].l+t[p].r)/2;
ll ans=0;
if( x<=mid ) ans+=query(p*2,x,y);
if( y>mid ) ans+=query(p*2+1,x,y);
return ans;
}
这这这……这个查询和更改就一起讲了,思路是差不多的,就是有一个懒惰标记需要理解理解,其实学学就会了
得了,不吹牛了,讲代码。看图
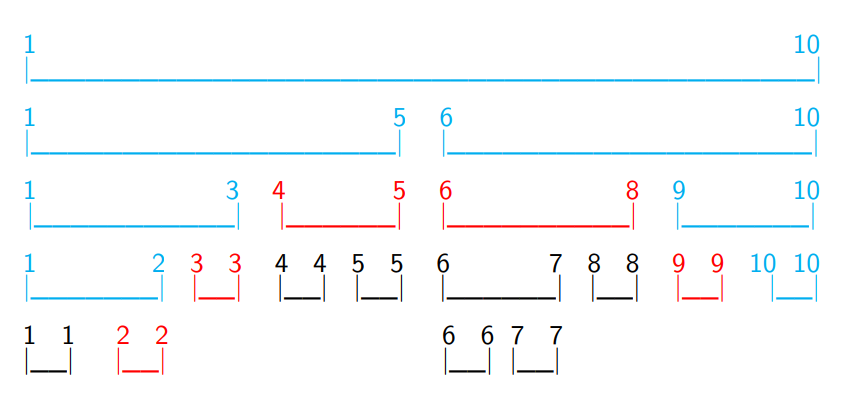
蓝色部分(除了10__10,那是标错了)是要查询或修改的祖先,红色部分是查询或修改的部分。如果没有lazy_tag,他的速度会大幅下降!!!
这是我们要查询or修改2~9的区间。
未使用lazy_tag,则被红色区域框起来(既4_4 5_5 6_7 8_8 6_6 7_7)的线段皆要更改,查询则是要查到最深,浪费时间。lazy_tag,就是用来降时间的。
它只需要查到或修改属于这段区间的区间。例如
2~9有1_3 4_5 6_8 9_10。其中13其中包括了23,所以1_3也要继续往下查。4、6都大于2 , 5、8都小于9,这里就做一个标记,表示下面要进行更改or查询。
9_10包括了9这个节点,却不在2~9中,所以要继续往下查。最后进行标记的有2_2 3_3 4_5 6_8 9_9。要注意,如果破坏这个作了标记的节点,tag要向下传递。
例如我要修改2_9,我给4_5和6_8加持了tag。而我要查询5~6,我就要把4_5和6_8继续查下去,那么4_5和6_8的tag就会破坏掉,而他的儿子就会加上一个tag。这就是lazy_tag。
他很好理解对不对?它的代码复杂度有点……低,但是理解它却不简单。